簡介

為了要了解如何用四元數推導出 3D 旋轉的公式，我找到了這篇文章 - 四元数与三维旋转 寫的相當詳細，這篇文章主要是希望跟著他一步步了解其中的推導過程，以後才不會對 3D 旋轉的矩陣公式為什麼是這樣寫而感到困惑

1. 三維空間中的旋轉

在探討四元數之前，我們先了解三維空間中旋轉的數學表示和推導過程

1.1 旋轉的分解

在推導旋轉公式之前，我們需要理解向量的分解。任何向量 $\mathbf{v}$ 都可以分解為兩個相互垂直的分量：

$$\mathbf{v} = \mathbf{v}_{\parallel} + \mathbf{v}_{\perp}$$

其中：

• 旋轉軸為 $\mathbf{u}$
• $\mathbf{v}_{\parallel}$ 是向量 $\mathbf{v}$ 在旋轉軸方向上的平行分量
• $\mathbf{v}_{\perp}$ 是向量 $\mathbf{v}$ 垂直於旋轉軸的分量

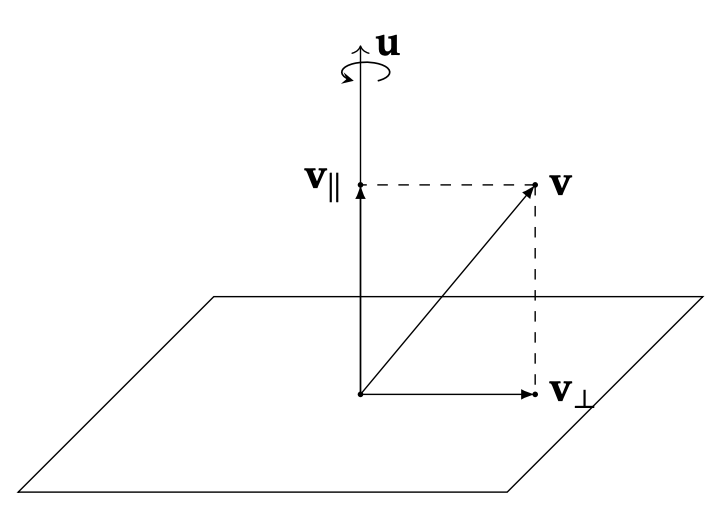
如上圖所示，在三維空間中，一個向量 $\mathbf{v}$ 對旋轉軸 $\mathbf{u}$ 的投影 $\mathbf{v}_{\parallel}$（平行分量）的計算公式如下：

$$\mathbf{v}_{\parallel} = \text{proj}_{\mathbf{u}}(\mathbf{v})$$

根據 向量的正射影 定義，此公式可以展開為：

$$= \frac{\mathbf{u} \cdot \mathbf{v}}{||\mathbf{u}||^2}\mathbf{u}$$

在三維空間的旋轉中，由於旋轉軸 $\mathbf{u}$ 的長度不是重點，我們在意的是旋轉軸其向量指向的方向，因此可以將旋轉軸 $\mathbf{u}$ 定義成單位向量，也就是：

$$||\mathbf{u}|| = \sqrt{x^2 + y^2 + z^2} = 1$$

如此可以將上述公式可以進一步簡化：

$$\mathbf{v}_{\parallel} = (\mathbf{u} \cdot \mathbf{v})\mathbf{u}$$

因為 $\mathbf{v} = \mathbf{v}_{\parallel} + \mathbf{v}_{\perp}$ ，所以：

$$\mathbf{v}_{\perp} = \mathbf{v} - (\mathbf{u} \cdot \mathbf{v})\mathbf{u}$$

現在我們知道如何將 $\mathbf{v}$ 分解成平行與垂直的分量，接下來要計算的是這兩個分量繞著 $\mathbf{u}$ 旋轉後的改變

1.2 $\mathbf{v}_{\parallel}$ 的旋轉

首先是 $\mathbf{v}_{\parallel}$ 的旋轉，由於其平行於旋轉軸 $\mathbf{u}$ 所以旋轉過後根本沒有改變，所以：

$$\mathbf{v}'_{\parallel} = \mathbf{v}_{\parallel}$$

1.3 $\mathbf{v}_{\perp}$ 的旋轉

接下來看的是與旋轉軸 $\mathbf{u}$ 垂直的 $\mathbf{v}_{\perp}$ 分量，以下是旋轉的示意圖，左側為 3D 視角下的旋轉、右側為由上往下看的 2D 視角，$\theta$ 為 $\mathbf{v}_{\perp}$ 分量逆時針繞著旋轉軸旋轉的角度

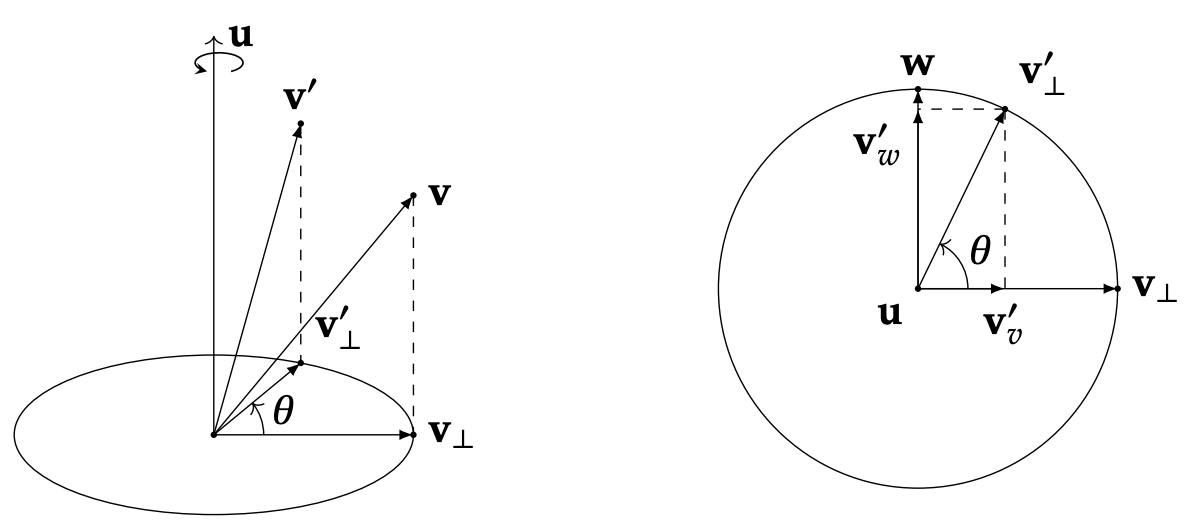
接著我們來看右圖 - 2D 平面上的旋轉，要求出旋轉後的 $\mathbf{v}’_\perp$ 需要的是兩個分量 $\mathbf{v}'_\mathbf{v}$ 跟 $\mathbf{v}'_\mathbf{w}$ ，而要求出 $\mathbf{v}'_\mathbf{w}$ 之前需要求的是 $\mathbf{w}$

向量 $\mathbf{w}$ 同時垂直於 $\mathbf{u}$ 以及 $\mathbf{v}_{\perp}$，這代表向量 $\mathbf{w}$ 可以通過兩者的外積取得：

$$
\mathbf{w} = \mathbf{u} \times \mathbf{v}_\perp
$$

P.S. 由於我們使用的是右手座標系統，所以 外積乘法的順序 是先 $\mathbf{u}$ 再 $\mathbf{v}_{\perp}$

根據 外積的幾何意義：

$$
||\mathbf{a}\times\mathbf{b}||
= ||\mathbf{a}||\ ||\mathbf{b}|| \sin(\theta)
$$

因此，向量 $\mathbf{w}$ 的長度可以表示為：

$$
||\mathbf{w}||
= ||\mathbf{u}||\ ||\mathbf{v}_\perp|| \sin(\pi/2)
$$

由於 $\mathbf{u}$ 是單位向量，上式可進一步化簡為：

$$
||\mathbf{w}|| = ||\mathbf{v}_\perp||
$$

這代表 $\mathbf{w}$ 與 $\mathbf{v}_\perp$ 的長度是相同的，並且兩者都位於同一個圓上

接著利用簡單的三角學計算：

$$ \begin{align*} \mathbf{v}'_{\perp} &= \mathbf{v}'_{v} + \mathbf{v}'_{w} \\[4pt] &= \cos(\theta)\mathbf{v}_{\perp} + \sin(\theta)\mathbf{w} \\[4pt] &= \cos(\theta)\mathbf{v}_{\perp} + \sin(\theta)(\mathbf{u} \times \mathbf{v}_{\perp}) \end{align*} $$

1.4 $\mathbf{v}$ 的旋轉

將上面平行與垂直分量的旋轉組合後：

$$ \begin{align*} \mathbf{v}' &= \mathbf{v}'_{\parallel} + \mathbf{v}'_{\perp} \\[4pt] &= \mathbf{v}_{\parallel} + \cos(\theta)\mathbf{v}_{\perp} + \sin(\theta)(\mathbf{u} \times \mathbf{v}_{\perp}) \end{align*} $$

由於外積遵守分配律：

$$ \begin{align*} \mathbf{u} \times \mathbf{v}_{\perp} &= \mathbf{u} \times (\mathbf{v} - \mathbf{v}_{\parallel}) \\[4pt] &= \mathbf{u} \times \mathbf{v} - \mathbf{u} \times \mathbf{v}_{\parallel} \\[4pt] &= \mathbf{u} \times \mathbf{v} \qquad (\mathbf{u} \ \text{平行於} \ \mathbf{v}_{\parallel}, \ \text{所以} \ \mathbf{u} \times \mathbf{v}_{\parallel} = 0) \end{align*} $$

最後將 $ \mathbf{v}_{\parallel} = (\mathbf{u} \cdot \mathbf{v})\mathbf{u} $ 與 $ \mathbf{v}_{\perp} = \mathbf{v} - (\mathbf{u} \cdot \mathbf{v})\mathbf{u} $ 代入：

$$ \begin{align*} \mathbf{v'} &= (\mathbf{u} \cdot \mathbf{v})\mathbf{u} + \cos(\theta)(\mathbf{v} - (\mathbf{u} \cdot \mathbf{v})\mathbf{u}) + \sin(\theta)(\mathbf{u} \times \mathbf{v}) \\[4pt] &= \cos(\theta)\mathbf{v} + (1 - \cos(\theta))(\mathbf{u} \cdot \mathbf{v})\mathbf{u} + \sin(\theta)(\mathbf{u} \times \mathbf{v}) \end{align*} $$

所求出的即是 羅德里格旋轉公式

2. 四元數

四元數的定義：

$$q = a + bi + cj + dk \quad (a, b, c, d \in \mathbb{R})$$

其中 $i, j, k$ 是虛數單位，滿足：

$$i^2 = j^2 = k^2 = ijk = -1$$

而四元數以向量形式表示如下：

$$ q = \begin{bmatrix} a \\ b \\ c \\ d \end{bmatrix} $$

另外，四元數經常將 實部($s$) 與 虛部($\mathbf{v}$) 分開，並用一個三維的向量表示虛部，這種表示方式稱為純量和向量的有序對形式：

$$ q = [s, \mathbf{v}] \quad \left(\mathbf{v} = \begin{bmatrix} x \\ y \\ z \end{bmatrix},\;s,x,y,z \in \mathbb{R}\right) $$

2.1 四元數的長度

四元數的長度，或者更精確的稱之為 範數，定義為：

$$
||q|| = \sqrt{a^2 + b^2 + c^2 + d^2}.
$$

如果以純量向量的有序對形式表示，$q = [s, \mathbf{v}]$ 的長度為：

$$ \begin{align*} ||q|| &= \sqrt{s^2 + \|\mathbf{v}\|^2} \\ &= \sqrt{s^2 + \mathbf{v} \cdot \mathbf{v}} \quad (\mathbf{v} \cdot \mathbf{v} = \|\mathbf{v}\|^2) \end{align*} $$

2.2 四元數的加法與減法

四元數的加法運算遵循分量相加的規則，對於兩個四元數：

$q_1 = a + bi + cj + dk$

$q_2 = e + fi + gj + hk$

它們的加法定義為：

$$ \begin{align*} q_1 + q_2 &= a + bi + cj + dk + e + fi + gj + hk \\ &= (a + e) + (b + f)i + (c + g)j + (d + h)k \end{align*} $$

同樣地，四元數的減法定義為：

$$
q_1 - q_2 = (a - e) + (b - f)i + (c - g)j + (d - h)k
$$

而以純量向量有序對形式表示的話，例如：$q_1 = [s, \mathbf{v}]$, $q_2 = [t, \mathbf{u}]$，則加減法運算為：

$$q_1 \pm q_2 = [s \pm t, \mathbf{v} \pm \mathbf{u}]$$

2.3 四元數的乘法

四元數的乘法是四元數運算中最複雜的部分，它不滿足交換律。對於兩個四元數：

$$q_1 = a + bi + cj + dk = [s, \mathbf{v}]$$
$$q_2 = e + fi + gj + hk = [t, \mathbf{u}]$$

其中：
$s = a \quad \mathbf{v} = (b, c, d)$
$t = e \quad \mathbf{u} = (f, g, h)$

2.3.1 基本乘法規則

四元數的乘法遵循以下規則：

$$i^2 = j^2 = k^2 = ijk = -1$$
$$ij = k, \quad ji = -k$$
$$ik = -j, \quad ki = j$$
$$jk = i, \quad kj = -i$$

四元數乘法表總結如下，左下的欄乘以右上的列會是表格中的結果，例如：$ij = k, \quad ji = -k$

×	1	i	j	k
1	1	i	j	k
i	i	-1	k	-j
j	j	-k	-1	i
k	k	j	-i	-1

2.3.2 展開式乘法

使用展開式計算 $q_1 \cdot q_2$：

$$ \begin{align*} q_1 q_2 &= (a + bi + cj + dk)(e + fi + gj + hk) \\ &= ae + afi + agj + ahk + \\ &\quad bei + bfi^2 + bgij + bhik + \\ &\quad cej + cfji + cgj^2 + chjk + \\ &\quad dek + dfki + dgkj + dhk^2 \end{align*} $$

利用 乘法規則 化簡：

$$ \begin{align*} q_1 q_2 &= ae + afi + agj + ahk + \\ &\quad bei - bf + bgk - bhj + \\ &\quad cej - cfk - cg + chi + \\ &\quad dek + dfj - dgi - dh \end{align*} $$

重新整理得到：

$$ \begin{align*} q_1 q_2 &= (a\textcolor{orangeRed}{e} - b\textcolor{deepskyblue}{f} - c\textcolor{green}{g} - d\textcolor{orange}{h}) + \\ &\quad (b\textcolor{orangeRed}{e} + a\textcolor{deepskyblue}{f} - d\textcolor{green}{g} + c\textcolor{orange}{h})i + \\ &\quad (c\textcolor{orangeRed}{e} + d\textcolor{deepskyblue}{f} + a\textcolor{green}{g} - b\textcolor{orange}{h})j + \\ &\quad (d\textcolor{orangeRed}{e} - c\textcolor{deepskyblue}{f} + b\textcolor{green}{g} + a\textcolor{orange}{h})k \end{align*} $$

2.3.3 矩陣形式

將以上展開式寫成矩陣形式為：

$$ q_1 q_2 = \begin{bmatrix} a & -b & -c & -d \\ b & a & -d & c \\ c & d & a & -b \\ d & -c & b & a \end{bmatrix} \begin{bmatrix} \textcolor{orangeRed}{e} \\ \textcolor{deepskyblue}{f} \\ \textcolor{green}{g} \\ \textcolor{orange}{h} \end{bmatrix} $$

以同樣的方式展開 $q_2 \cdot q_1$，可得：

$$ q_2 q_1 = \begin{bmatrix} a & -b & -c & -d \\ b & a & d & -c \\ c & -d & a & b \\ d & c & -b & a \end{bmatrix} \begin{bmatrix} \textcolor{orangeRed}{e} \\ \textcolor{deepskyblue}{f} \\ \textcolor{green}{g} \\ \textcolor{orange}{h} \end{bmatrix} $$

2.3.4 Grassmann product

讓我們將前面 $q_1 \cdot q_2$ 的展開重新整理一下：

$$ \begin{align*} q_1 q_2 &= (ae - (b\textcolor{deepskyblue}{f} + c\textcolor{deepskyblue}{g} + d\textcolor{deepskyblue}{h})) + \\ &\quad (a\textcolor{deepskyblue}{f} + e\textcolor{orangeRed}{b} + ch - dg)i + \\ &\quad (a\textcolor{deepskyblue}{g} + e\textcolor{orangeRed}{c} + df - bh)j + \\ &\quad (a\textcolor{deepskyblue}{h} + e\textcolor{orangeRed}{d} + bg - cf)k \end{align*} $$

如果令 $\mathbf{v} = \begin{bmatrix} b \\ c \\ d \end{bmatrix}$, $\mathbf{u} = \begin{bmatrix} f \\ g \\ h \end{bmatrix}$ ，那麼：

$$\mathbf{v} \cdot \mathbf{u} = bf + cg + dh$$

$$\mathbf{v} \times \mathbf{u} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ b & c & d \\ f & g & h \end{vmatrix} = (ch - dg)\mathbf{i} - (bh - df)\mathbf{j} + (bg - cf)\mathbf{k}$$

如此一來，上面的 $q_1 \cdot q_2$ 可以化簡為：

$$ q_1 q_2 = [ae - \mathbf{v} \cdot \mathbf{u}, a\mathbf{u} + e\mathbf{v} + \mathbf{v} \times \mathbf{u}] $$

這個結果就被稱為 Grassmann product

總結來說，以純量向量形式表達的任意四元數 $q_1 = [s, \mathbf{v}]$, $q_2 = [t, \mathbf{u}]$，$q_1q_2$ 的結果是：

$$
q_1 q_2 = [st - \mathbf{v} \cdot \mathbf{u}, s\mathbf{u} + t\mathbf{v} + \mathbf{v} \times \mathbf{u}]
$$

2.4 純四元數

純四元數（Pure Quaternion） 是指實部為零的四元數，即：

$$q = 0 + xi + yj + zk = [0, \mathbf{v}]$$

其中 $\mathbf{v} = (x, y, z)$ 是一個三維向量

而純四元數有一個很重要的特性，如果有兩個純四元數 $v=[0, \mathbf{v}]$, $u=[0, \mathbf{u}]$，兩者的乘積可以套用 Grassmann product 計算：

$$ \begin{align*} vu &= [0 -\mathbf{v} \cdot \mathbf{u}, 0 + \mathbf{v} \times \mathbf{u}] \\ &= [-\mathbf{v} \cdot \mathbf{u}, \mathbf{v} \times \mathbf{u}] \end{align*} $$

2.5 四元數的逆和共軛

2.5.1 逆和共軛的定義

四元數 $q$ 的 逆(Inverse) $q^{-1}$ 定義如下：

$$qq^{-1} = q^{-1}q = 1 \quad (q \neq 0)$$

四元數 $q = a + bi + cj + dk$ 的 共軛(Conjugate) $q^{*}$ 定義如下：

$$q^* = a - bi - cj - dk$$

如果是以純量向量有序對的形式表示，四元數 $q = [s, \mathbf{v}]$，其 共軛(Conjugate)

$$q^{*} = [s, \mathbf{-v}]$$

2.5.2 共軛與範數的關係

讓我們利用 Grassmann product 來計算 $qq^*$：

$$ \begin{align*} qq^* &= [s, \mathbf{v}] \cdot [s, -\mathbf{v}] \\ &= [s^2 - \mathbf{v} \cdot (-\mathbf{v}), s(-\mathbf{v}) + s\mathbf{v} + \mathbf{v} \times (-\mathbf{v})] \\ &= [s^2 + \mathbf{v} \cdot \mathbf{v}, 0] \end{align*} $$

（$\mathbf{v}$ 平行於 $-\mathbf{v}$，所以 $\mathbf{v} \times (-\mathbf{v}) = 0$）

可以看到，這最終的結果是一個實數，而它正是四元數長度的平方：

$$ \begin{align*} qq^* &= [s^2 + \mathbf{v} \cdot \mathbf{v}, 0] \\ &= s^2 + x^2 + y^2 + z^2 \\ &= \|q\|^2 \end{align*} $$

因為 $(q^*)^* = [s, -(-\mathbf{v})] = [s, \mathbf{v}] = q$ ，所以：

$$ \begin{align*} q^*q &= (q^*)(q^*)^* \\ &= \|q^*\|^2 \quad (\text{將上面} \ qq^* \text{的} \ q \ \text{代入} \ q^*) \\ &= s^2 + x^2 + y^2 + z^2 \\ &= \|q\|^2 \\ &= qq^* \end{align*} $$

所以可以得到 $q^*q = qq^*$ ，這個特殊的乘法是遵守交換律的

2.5.3 利用共軛求得四元數的逆

基於上述結果，我們可以推導四元數的逆。從逆的定義開始：

$$qq^{-1} = 1$$

等式兩邊同時左乘以 $q^*$：

$$q^*qq^{-1} = q^*$$

利用結合律：

$$(q^*q)q^{-1} = q^*$$

因為 $q^*q = ||q||^2$：

$$||q||^2 \cdot q^{-1} = q^*$$

兩邊同時除以 $||q||^2$：

$$q^{-1} = \frac{q^*}{||q||^2}$$

用這種方法尋找四元數的逆非常方便，只需要將其虛部改變符號，再除以其長度的平方就可以找到逆了

如果 $q$ 是單位四元數（$||q|| = 1$），那麼其逆就等於其共軛：

$$q^{-1} = q^*$$

3. 四元數與 3D 旋轉

瞭解了三維空間中的旋轉與四元數的基本知識，終於可以將四元數與 3D 旋轉之間的關係串起來了！

三維空間中的旋轉 描述一個三維的向量 $\mathbf{v}$ 繞著旋轉軸 $\mathbf{u}$ 旋轉 $\theta$ 度，可以將其拆分為垂直於旋轉軸的 $\mathbf{v}_{\perp}$ 以及平行於旋轉軸的 $\mathbf{v}_{\parallel}$ ，我們對這兩個向量分別進行旋轉，獲得 $\mathbf{v'}_{\perp}$ 及 $\mathbf{v'}_{\parallel}$ ，將它們相加後得到 $\mathbf{v}$ 旋轉後的結果 $\mathbf{v'} = \mathbf{v'}_{\perp} + \mathbf{v'}_{\parallel}$

我們打算將這些三維的向量以純四元數表示：

$$v = [0, \mathbf{v}]$$ $$v_{\perp} = [0, \mathbf{v}_{\perp}]$$ $$v_{\parallel} = [0, \mathbf{v}_{\parallel}]$$ $$u = [0, \mathbf{u}]$$

以及旋轉後的向量：

$$v' = [0, \mathbf{v}']$$ $$v'_{\perp} = [0, \mathbf{v}'_{\perp}]$$ $$v'_{\parallel} = [0, \mathbf{v}'_{\parallel}]$$

那麼我們可以得到：

$$v = v_{\perp} + v_{\parallel}$$ $$v' = v'_{\perp} + v'_{\parallel}$$

接著和 三維空間中的旋轉 章節中做的事情一樣，我們將分別討論 $v_{\perp}$ 和 $v_{\parallel}$ 的狀況

3.1 $v’_{\perp}$ 的旋轉

三維空間中 $\mathbf{v}_{\perp}$ 的旋轉 中推導過：

$$ \mathbf{v}'_{\perp} = \cos(\theta)\mathbf{v}_{\perp} + \sin(\theta)(\mathbf{u} \times \mathbf{v}_{\perp}) $$

我們可以將以上的三維向量 $\mathbf{v}'_{\perp}$ 和 $\mathbf{v}_{\perp}$ 替換成純四元數 $v'_{\perp}$ 和 $v_{\perp}$ ：

$$ v'_{\perp} = \cos(\theta)v_{\perp} + \sin(\theta)(\mathbf{u} \times v_{\perp}) $$

接下來我們想要把 $\mathbf{u} \times v_{\perp}$ 替換掉：

純四元數 章節中推導過，兩個純四元數 $v=[0, \mathbf{v}]$, $u=[0, \mathbf{u}]$ 的乘積計算如下：

$$ vu = [-\mathbf{v} \cdot \mathbf{u}, \mathbf{v} \times \mathbf{u}] $$

這裡我們將兩個純四元數替換成 $u = [0, \mathbf{u}]$ 及 $v_{\perp} = [0, \mathbf{v}_{\perp}]$：

$$ \begin{align*} uv_{\perp} &= [-\mathbf{u} \cdot v_{\perp}, \mathbf{u} \times v_{\perp}] \\[4pt] &= [0, \mathbf{u} \times v_{\perp} ] \quad (因為 \ v_{\perp} 垂直於 \ \mathbf{u} \ 所以兩者內積等於 0) \\[4pt] &= \mathbf{u} \times v_{\perp} \end{align*} $$

將 $\mathbf{u} \times v_{\perp}$ 替換掉後，$ v_{\perp} $ 等於：

$$ \begin{align*} v'_{\perp} &= \cos(\theta)v_{\perp} + \sin(\theta)(uv_{\perp}) \\[4pt] &= (\cos(\theta) + \sin(\theta)u)v_{\perp} \quad (由於四元數乘法遵守分配律) \end{align*} $$

如果我們將 $\cos(\theta) + \sin(\theta)u$ 看做是一個四元數 $q = \cos(\theta) + \sin(\theta)u$，進一步可以將 $v’_{\perp}$ 表示為：

$$ v'_{\perp} = qv_{\perp} $$

更進一步，我們可以將 $q$ 表示為純量向量有序對形式：

$$ \begin{align*} q &= \cos(\theta) + \sin(\theta)u \\[4pt] &= [\cos(\theta), \mathbf{0}] + [0, \sin(\theta)\mathbf{u}] \\[4pt] &= [\cos(\theta), \sin(\theta)\mathbf{u}] \end{align*} $$

如此一來我們就求出了旋轉後 $v’$ 的表示方式：

$$ v'_{\perp} = qv_{\perp} $$

其中：

$q = [\cos(\theta), \sin(\theta)\mathbf{u}]$

$v_{\perp} = [0, \mathbf{v}_{\perp}]$

額外補充，這個四元數 $q$ 還有一個重要的性質 - 其實他是一個單位四元數，證明如下：

$$ \begin{alignat*}{2} \|q\| &= \sqrt{\cos^2(\theta) + (\sin(\theta)\mathbf{u} \cdot \sin(\theta)\mathbf{u})} \\ &= \sqrt{\cos^2(\theta) + \sin^2(\theta)(\mathbf{u} \cdot \mathbf{u})} \\ &= \sqrt{\cos^2(\theta) + \sin^2(\theta)(\|\mathbf{u}\|^2)} &\quad (\mathbf{u} \cdot \mathbf{u} = \|\mathbf{u}\|^2) \\ &= \sqrt{\cos^2(\theta) + \sin^2(\theta)} &\quad (\mathbf{u} \text{ 是單位向量，因此 } \|\mathbf{u}\| = 1) \\ &= 1 &\quad (\text{三角恒等式}) \end{alignat*} $$

3.2 $v’_{\parallel}$ 的旋轉

對於平行於旋轉軸的分量 $v_{\parallel}$，由於其平行於旋轉軸 $u$，旋轉後不會改變：

$$v'_{\parallel} = v_{\parallel}$$

3.3 $v’$ 的旋轉

結合 $v_{\perp}$ 和 $v_{\parallel}$ 的旋轉結果：

$$ \begin{align*} v' &= v'_{\parallel} + v'_{\perp} \\[4pt] &= v_{\parallel} + qv_{\perp} \quad (其中 \ q = [\cos(\theta), \sin(\theta)\mathbf{u}]) \end{align*} $$

再繼續往下化簡前，我們需要先證明 引理 1

3.3.1 引理 1

引理 1 要證明的是：

如果 $q = [\cos(\theta), \sin(\theta)\mathbf{u}]$，而且 $\mathbf{u}$ 為單位向量，那麼 $q^2 = qq = [\cos(2 \theta), \sin(2 \theta)\mathbf{u}]$

證明如下：

$q = [\cos(\theta), \sin(\theta)\mathbf{u}]$，我們可以求得 $q^2$ 為：

$$ \begin{alignat*}{2} q^2 &= [\cos(\theta), \sin(\theta)\mathbf{u}] \cdot [\cos(\theta), \sin(\theta)\mathbf{u}] &\quad (1) \\[6pt] &= [\cos^2(\theta) - (\sin(\theta)\mathbf{u} \cdot \sin(\theta)\mathbf{u}), (\cos(\theta)\sin(\theta) + \sin(\theta)\cos(\theta))\mathbf{u} + (\sin(\theta)\mathbf{u} \times \sin(\theta)\mathbf{u})] &\quad (2) \\[6pt] &= [\cos^2(\theta) - \sin^2(\theta)\|\mathbf{u}\|^2, 2\sin(\theta)\cos(\theta)\mathbf{u} + 0] &\quad (3) \\[6pt] &= [\cos^2(\theta) - \sin^2(\theta), 2\sin(\theta)\cos(\theta)\mathbf{u}] &\quad (4) \\[6pt] &= [\cos(2\theta), \sin(2\theta)\mathbf{u}] &\quad (5) \\[6pt] \end{alignat*} $$

其中各個步驟：

(1) => (2)，使用了 Grassmann product
(2) => (3)，$\mathbf{u} \cdot \mathbf{u} = ||\mathbf{u}^2||$ 及 $\mathbf{u} \times \mathbf{u} = 0$
(3) => (4)，由於 $\mathbf{u}$ 是單位向量，$||\mathbf{u}|| = 1$
(4) => (5)，使用了 二倍角公式

引理 1 的幾何意義其實代表了如果繞著旋轉軸 $\mathbf{u}$ 連續旋轉 $\theta$ 度兩次，所做出的變換其實等同繞著 $\mathbf{u}$ 旋轉了兩倍的度數 ($2\theta$)

接著我們引入一個新的四元數 $p$：

$$p = [\cos(\frac{1}{2}\theta), \sin(\frac{1}{2}\theta)\mathbf{u}]$$

這個四元數 $p$ 與之前的 $q$ 的關係是：

$$ \begin{align*} p^2 &= [\cos(2 \cdot \frac{1}{2}\theta), \sin(2 \cdot \frac{1}{2}\theta)\mathbf{u}] \\[4pt] &= [\cos(\theta), \sin(\theta)\mathbf{u}] \\[4pt] &= q \end{align*} $$

和 $q$ 一樣，$p$ 也是一個單位四元數 ($||p|| = 1$)，因此其 逆等於共軛：

$$
p^{-1} = p^{*}
$$

最後，推導出來的 引理 1 可以將 v’ 的旋轉公式 表示為：

$$ \begin{align*} v' &= v_{\parallel} + qv_{\perp} \\[4pt] &= 1 \cdot v_{\parallel} + qv_{\perp} \\[4pt] &= pp^{-1}v_{\parallel} + ppv_{\perp} \\[4pt] &= pp^{*}v_{\parallel} + ppv_{\perp} \end{align*} $$

這裡我們需要暫停一下，先證明 引理 2 及 引理 3 後再繼續化簡

3.3.2 引理 2

引理 2 要證明的是：

假設 $v_{\parallel} = [0, \mathbf{v}_{\parallel}]$ 是一個純四元數，而 $q = [\alpha, \beta\mathbf{u}] \ (\alpha, \beta \in \mathbb{R})$，其中 $\mathbf{u}$ 是一個單位向量
在這種條件下，如果 $\mathbf{v}_{\parallel}$ 平行於 $\mathbf{u}$，那麼 $qv_{\parallel} = v_{\parallel}q$

這個引理需要用到 Grassmann product，證明的方式如下：

首先先計算等式左邊：

$$ \begin{align*} qv_{\parallel} &= [\alpha, \beta\mathbf{u}] \cdot [0, \mathbf{v}_{\parallel}] \\[4pt] &= [0 - \beta\mathbf{u} \cdot \mathbf{v}_{\parallel}, \alpha\mathbf{v}_{\parallel} + 0 + \beta\mathbf{u} \times \mathbf{v}_{\parallel}] \\[4pt] &= [-\beta\mathbf{u} \cdot \mathbf{v}_{\parallel}, \alpha\mathbf{v}_{\parallel}] \quad (\mathbf{v}_{\parallel} \text{平行於} \ \mathbf{u}, \text{所以} \ \beta\mathbf{u} \times \mathbf{v}_{\parallel} = 0) \end{align*} $$

接著計算等式右邊：

$$ \begin{align*} v_{\parallel}q &= [0, \mathbf{v}_{\parallel}] \cdot [\alpha, \beta\mathbf{u}] \\[4pt] &= [0 - \mathbf{v}_{\parallel} \cdot \beta\mathbf{u}, 0 + \alpha\mathbf{v}_{\parallel} + \mathbf{v}_{\parallel} \times \beta\mathbf{u}] \\[4pt] &= [-\mathbf{v}_{\parallel} \cdot \beta\mathbf{u}, \alpha\mathbf{v}_{\parallel}] \quad (\mathbf{v}_{\parallel} \text{平行於} \ \mathbf{u}, \text{所以} \ \mathbf{v}_{\parallel} \times \beta\mathbf{u} = 0) \\[4pt] &= [-\beta\mathbf{u} \cdot \mathbf{v}_{\parallel}, \alpha\mathbf{v}_{\parallel}] \quad (\text{內積遵守交換律}) \end{align*} $$

等式左邊 = 等式右邊，引理得證

3.3.3 引理 3

引理 3 要證明的是：

假設 $v_{\perp} = [0, \mathbf{v}_{\perp}]$ 是一個純四元數，而 $q = [\alpha, \beta\mathbf{u}] \ (\alpha, \beta \in \mathbb{R})$，其中 $\mathbf{u}$ 是一個單位向量
在這種條件下，如果 $\mathbf{v}_{\perp}$ 正交於 $\mathbf{u}$ ，那麼 $qv_{\perp} = v_{\perp}q^*$

這個引理同樣需要用到 Grassmann product，證明的方式如下：

首先計算等式左邊：

$$ \begin{align*} qv_{\perp} &= [\alpha, \beta\mathbf{u}] \cdot [0, \mathbf{v}_{\perp}] \\[4pt] &= [0 - \beta\mathbf{u} \cdot \mathbf{v}_{\perp}, \alpha\mathbf{v}_{\perp} + 0 + \beta\mathbf{u} \times \mathbf{v}_{\perp}] \\[4pt] &= [0, \alpha\mathbf{v}_{\perp} + \beta\mathbf{u} \times \mathbf{v}_{\perp}] \quad (\mathbf{v}_{\perp} \text{正交於} \ \mathbf{u}, \text{所以} \ \beta\mathbf{u} \cdot \mathbf{v}_{\perp} = 0) \end{align*} $$

接著計算等式右邊：

$$ \begin{align*} v_{\perp}q^* &= [0, \mathbf{v}_{\perp}] \cdot [\alpha, -\beta\mathbf{u}] \\[4pt] &= [0 - \mathbf{v}_{\perp} \cdot (-\beta\mathbf{u}), 0 + \alpha\mathbf{v}_{\perp} + \mathbf{v}_{\perp} \times (-\beta\mathbf{u})] \\[4pt] &= [\beta\mathbf{u} \cdot \mathbf{v}_{\perp}, \alpha\mathbf{v}_{\perp} - \beta\mathbf{v}_{\perp} \times \mathbf{u}] \\[4pt] &= [0, \alpha\mathbf{v}_{\perp} + \beta\mathbf{u} \times \mathbf{v}_{\perp}] \quad (\mathbf{v}_{\perp} \text{正交於} \ \mathbf{u}, \text{所以} \ \beta\mathbf{u} \cdot \mathbf{v}_{\perp} = 0, \text{且} \ \mathbf{v}_{\perp} \times \mathbf{u} = -\mathbf{u} \times \mathbf{v}_{\perp}) \end{align*} $$

等式左邊 = 等式右邊，引理得證

3.4 四元數的 3D 旋轉公式

必要的引理都證明完了，下面我們回到 引理 1 推導出的 $v’$：

$$ \begin{align*} v' &= v_{\parallel} + qv_{\perp} \\[4pt] &= 1 \cdot v_{\parallel} + qv_{\perp} \\[4pt] &= pp^{-1}v_{\parallel} + ppv_{\perp} \\[4pt] &= pp^{*}v_{\parallel} + ppv_{\perp} \end{align*} $$

然後套用

• 引理 2： $p^{*}v_{\parallel} = v_{\parallel}p^{*}$
• 引理 3：$pv_{\perp} = v_{\perp}p^{*}$

將 $v’$ 進一步化簡：

$$ \begin{align*} v' &= pp^{*}v_{\parallel} + ppv_{\perp} \\[4pt] &= pv_{\parallel}p^{*} + pv_{\perp}p^{*} \\[4pt] &= p(v_{\parallel} + v_{\perp})p^{*} \\[4pt] &= pvp^{*} \end{align*} $$

最終，我們得到了四元數 3D 旋轉的標準公式：

$$v’ = qvq^{*}$$

其中：

• $q = [\cos(\frac{1}{2}\theta), \sin(\frac{1}{2}\theta)\mathbf{u}]$ 是旋轉四元數
• $v = [0, \mathbf{v}]$ 是要旋轉的向量（表示為純四元數）
• $v’ = [0, \mathbf{v}’]$ 是旋轉後的向量（表示為純四元數）
• $\mathbf{u}$ 是旋轉軸（單位向量）
• $\theta$ 是旋轉角度

3.5 3D 旋轉的矩陣形式

前面在 四元數的乘法 - 矩陣形式 章節中推導過：

一個四元數 $v$ 左乘另一個四元數 $q = a+bi+cj+dk$，等同於下面這個矩陣：

$$ L(q) = \begin{bmatrix} a & -b & -c & -d \\ b & a & -d & c \\ c & d & a & -b \\ d & -c & b & a \end{bmatrix} $$

即 $qv = L(q)v$

而右乘 $q$ 等同於這個矩陣：

$$ R(q) = \begin{bmatrix} a & -b & -c & -d \\ b & a & d & -c \\ c & -d & a & b \\ d & c & -b & a \end{bmatrix} $$

即 $vq = R(q)v$

假設 $a = \cos\left(\frac{1}{2}\theta\right)$，$b = \sin\left(\frac{1}{2}\theta\right)u_x$，$c = \sin\left(\frac{1}{2}\theta\right)u_y$，$d = \sin\left(\frac{1}{2}\theta\right)u_z$，$q = a + bi + cj + dk$

接著我們可以將四元數 3D 旋轉的標準公式 $v’ = qvq^{*}$ 用上面這兩個矩陣相乘出來：

$$ \begin{align*} qvq^{*} &= L(q)R(q^{*})v \\[4pt] &=R(q^{*})L(q)v \quad (\text{由於四元數乘法遵守結合律所以它們是等價的}) \end{align*} $$

然後計算這兩個矩陣的相乘：

$$ \begin{align*} L(q)R(q^{*}) &= \begin{bmatrix} a & -b & -c & -d \\ b & a & -d & c \\ c & d & a & -b \\ d & -c & b & a \end{bmatrix} \begin{bmatrix} a & b & c & d \\ -b & a & -d & c \\ -c & d & a & -b \\ -d & -c & b & a \end{bmatrix} \\[4pt] &= \begin{bmatrix} a^2 + b^2 + c^2 + d^2 & ab - ab - cd + cd & ac + bd - ac - bd & ad - bc + bc - ad \\ ab - ab + cd - cd & b^2 + a^2 - d^2 - c^2 & bc - ad - ad + bc & bd + ac + bd + ac \\ ac - bd - ac + bd & bc + ad + ad + bc & c^2 - d^2 + a^2 - b^2 & cd + cd - ab - ab \\ ad + bc - bc - ad & bd - ac + bd - ac & cd + cd + ab + ab & d^2 - c^2 - b^2 + a^2 \end{bmatrix} \end{align*} $$

在 $v’_{\parallel}$ 的旋轉 章節的最後，證明過 $q$ 是單位四元數，因此 $a^2 + b^2 + c^2 + d^2 = 1$，進一步化簡後得到：

$$ L(q)R(q^{*}) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1-2(c^2+d^2) & 2(bc-ad) & 2(ac+bd) \\ 0 & 2(bc+ad) & 1-2(b^2+d^2) & 2(cd-ab) \\ 0 & 2(bd-ac) & 2(ab+cd) & 1-2(b^2+c^2) \end{bmatrix} $$

最終可以求得：

$$ v' = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1-2(c^2+d^2) & 2(bc-ad) & 2(ac+bd) \\ 0 & 2(bc+ad) & 1-2(b^2+d^2) & 2(cd-ab) \\ 0 & 2(bd-ac) & 2(ab+cd) & 1-2(b^2+c^2) \end{bmatrix} v $$

由於矩陣的最外圈不會對 $v$ 造成任何變換，因此我們可以將它壓縮成 3 × 3 的矩陣，最終獲得由四元數推導而來的 3D 旋轉矩陣！

3D 旋轉矩陣

任意向量 $\mathbf{v}$ 沿著以單位向量定義的旋轉軸 $\mathbf{u}$ 旋轉 $\theta$ 角度之後的 $\mathbf{v}'$ 可以使用矩陣乘法來獲得

令 $a = \cos\left(\frac{1}{2}\theta\right)$，$b = \sin\left(\frac{1}{2}\theta\right)u_x$，$c = \sin\left(\frac{1}{2}\theta\right)u_y$，$d = \sin\left(\frac{1}{2}\theta\right)u_z$ $$ \mathbf{v}' = \begin{bmatrix} 1 - 2c^2 - 2d^2 & 2bc - 2ad & 2ac + 2bd \\ 2bc + 2ad & 1 - 2b^2 - 2d^2 & 2cd - 2ab \\ 2bd - 2ac & 2ab + 2cd & 1 - 2b^2 - 2c^2 \end{bmatrix} \mathbf{v} $$

4. 相關應用

4.1 Three.js

在 Three.js 中，makeRotationFromQuaternion 負責將四元數轉換為旋轉矩陣，其中的計算公式就是我們最後推導出的 3D 旋轉矩陣

4.1.1 基本用法

// 建立一個四元數：繞 Z 軸旋轉 90 度
const axis = new THREE.Vector3(0, 0, 1);
const angle = Math.PI / 2;
const q = new THREE.Quaternion().setFromAxisAngle(axis, angle);

// 把四元數轉換成 Matrix4
const m = new THREE.Matrix4().makeRotationFromQuaternion(q);

// 將 [1, 0, 0] 沿著 z 軸旋轉 90 度
const v = new THREE.Vector3(1, 0, 0);
v.applyMatrix4(m);
console.log(v); // [0, 1, 0] => 沒錯，[1,0,0] 被旋轉 90° 到 [0,1,0] (指向 Y 軸)

4.1.2 內部實現原理

makeRotationFromQuaternion 原始碼

makeRotationFromQuaternion( q ) {
  return this.compose( _zero, q, _one );
}

compose( position, quaternion, scale ) {
  const te = this.elements;

  const x = quaternion._x, y = quaternion._y, z = quaternion._z, w = quaternion._w;
  const x2 = x + x,	y2 = y + y, z2 = z + z;
  const xx = x * x2, xy = x * y2, xz = x * z2;
  const yy = y * y2, yz = y * z2, zz = z * z2;
  const wx = w * x2, wy = w * y2, wz = w * z2;

  const sx = scale.x, sy = scale.y, sz = scale.z;

  te[ 0 ] = ( 1 - ( yy + zz ) ) * sx;
  te[ 1 ] = ( xy + wz ) * sx;
  te[ 2 ] = ( xz - wy ) * sx;
  te[ 3 ] = 0;

  te[ 4 ] = ( xy - wz ) * sy;
  te[ 5 ] = ( 1 - ( xx + zz ) ) * sy;
  te[ 6 ] = ( yz + wx ) * sy;
  te[ 7 ] = 0;

  te[ 8 ] = ( xz + wy ) * sz;
  te[ 9 ] = ( yz - wx ) * sz;
  te[ 10 ] = ( 1 - ( xx + yy ) ) * sz;
  te[ 11 ] = 0;

  te[ 12 ] = position.x;
  te[ 13 ] = position.y;
  te[ 14 ] = position.z;
  te[ 15 ] = 1;

  return this;
}

可以看到 Line 16:29 使用的就是我們最後推導出來的 3D 旋轉矩陣

將 Three.js 的實現與我們推導的公式對應：

• x, y, z, w 對應四元數的 $b, c, d, a$ 分量
• x2, y2, z2 對應 $2b, 2c, 2d$

例如：

• te[0] = 1 - (yy + zz) 對應 $1 - 2c^2 - 2d^2$
• te[4] = xy - wz 對應 $2bc - 2ad$

4.2 3D Gaussian Splatting

3D 高斯潑濺法 (3D Gaussian Splatting, 3DGS) 是最近非常流行的 3D 重建技術，在 原始的論文 中也使用到了 3D 旋轉矩陣

4.2.1 3DGS 的核心概念

在 3DGS 中，一個 3D 場景是由數百萬個獨立的高斯球 (Gaussian) 所組成。每個高斯球都是一個帶有特定參數的 3D 橢圓體，這些參數決定了它的位置、大小、形狀和顏色

其中，最關鍵的參數是：

• 位置 ($\mathbf{\mu}$)：高斯球的中心點坐標
• 協方差矩陣 ($\Sigma$)：描述高斯球的形狀和方向

這個協方差矩陣 $\Sigma$ 可以進一步分解，這正是 3D 旋轉矩陣與四元數發揮作用的地方

4.2.2 協方差矩陣與旋轉

一個 3D 高斯球的協方差矩陣 $\Sigma$ 描述了它在三維空間中的橢球形狀。這個矩陣可以被分解為兩個部分：

$$\Sigma = R S S^T R^T$$

其中：

• $R$ 是 3D 旋轉矩陣 (3D Rotation Matrix)，決定了高斯球在空間中的方向
• $S$ 是 3D 縮放矩陣 (3D Scaling Matrix)，決定了高斯球沿著其主軸的長度

4.2.3 旋轉矩陣 R

在論文的 附錄 A - DETAILS OF GRADIENT COMPUTATION 中寫到，對於四元數 $q = q_r + q_{i}i + q_{j}j + q_{k}k$ ，其 旋轉矩陣 R 定義如下：

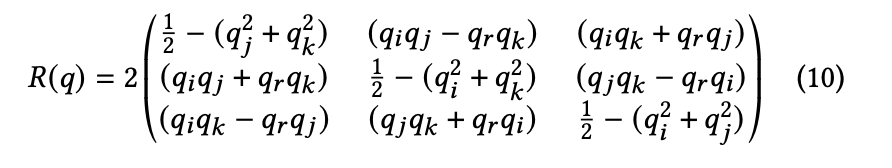
可以看到以上公式即為我們最終推導出來的 3D 旋轉矩陣

5. 參考資料

四元数与三维旋转

- 向量的正射影

【公式】正射影公式推導
高中數學 | 正射影(正射影長度)🔥 | 觀念詳細解析

- 維基百科

外積
引理