此為 機器學習中的優化器 系列文章 - 第 3 篇:
- 機器學習中的優化器 (1) - Gradient descent 梯度下降與其變體
- 機器學習中的優化器 (2) - 從梯度下降問題到動量優化
- 機器學習中的優化器 (3) - AdaGrad、RMSProp 與 Adam
前言
上篇文章提到 動量(Momentum) 的引入可以有效逃離局部最小值進而幫助找到全局的最佳解,但 Momentum 對所有的參數都套用同樣的學習率,導致在某些狀況下可能過度衝刺而不易找到全局最佳解。因此後來出現了一些優化算法 - AdaGrad, RMSProp, Adam 等讓學習率可以隨著訓練迭代的過程中自適應調整以更快的找到全局最佳解
什麼是 AdaGrad?
AdaGrad(Adaptive Gradient Algorithm) 是一種自適應學習率的優化算法,由 John Duchi 等人在 2011 年提出。它的核心思想是根據每個參數的歷史梯度來動態調整學習率。
數學表達式
標準梯度下降:
$$w_{t+1} = w_t - \eta \cdot g^t$$
其中:
- $w_t$ 是第 $t$ 步的權重
- $\eta$ 是學習率(步長)
- $g^t$ 是第 $t$ 步的梯度
AdaGrad:
$$w_i^{t+1} = w_i^t - \frac{\eta}{\sqrt{G_i^t + \epsilon}} \cdot g_i^t$$
其中:
- $w_i^{t+1}$ 是參數 $i$ 在第 $t+1$ 步的更新值
- $w_i^t$ 是參數 $i$ 在第 $t$ 步的當前值
- $\eta$ 是全局學習率
- 分母除以的 $\sqrt{G_i^t + \epsilon}$ 用來動態改變學習率
- $g_i^t$ 是參數 $i$ 在第 $t$ 步的梯度
- $\epsilon$ 是一個很小的常數(通常為 $10^{-8}$),用於避免分母除以零導致錯誤
上標 $t$ 代表的是第 t 步計算出來的值,下標 $i$ 指的是某個特定的參數。AdaGrad 的學習率是拿原本的學習率 $\eta$ 除以 $\sqrt{G_i^t + \epsilon}$,也就是說新的學習率現在不是固定的了,會隨著迭代的次數而動態改變
接著來看關鍵的 $G_i^t$,代表的是參數 $i$ 的梯度累積平方和:
$$G_i^t = G_i^{t-1} + (g_i^t)^2$$
其中:
- $G_i^t$ 是參數 $i$ 在第 $t$ 步的梯度累積平方和
- $G_i^{t-1}$ 是參數 $i$ 在第 $t-1$ 步的梯度累積平方和
- $g_i^t$ 是參數 $i$ 在第 $t$ 步的梯度
實際上 梯度累積平方和 是怎麼計算的呢?推薦這段影片 - 李宏毅老師講解 Root Mean Square 有清晰的講解
學習率自適應
AdaGrad 的關鍵創新在於學習率的自適應調整:
$$\eta_{AdaGrad} = \frac{\eta}{\sqrt{G_i^t + \epsilon}}$$
對於每個參數 $i$,其學習率會根據該參數的歷史梯度大小進行調整:
- 如果某個參數的梯度一直很小,$G_i^t$ 會累積得較小,學習率相對較大
- 如果某個參數的梯度一直很大,$G_i^t$ 會累積得很大,導致學習率變小
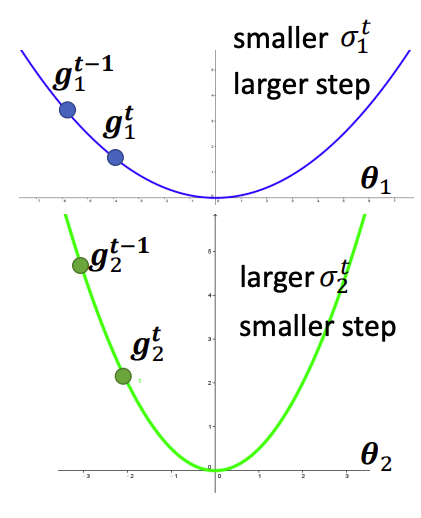
以下圖範例來看:
- 上方的藍線在從左至右迭代的過程中,Gradient 比較平緩也就是 $G_i^t$ 會累積得較小,此時學習率相對較大,參數更新的步伐也較大
- 下方的綠線在從左至右迭代的過程中,Gradient 比較陡峭也就是 $G_i^t$ 會累積得較大,此時學習率相對較小,參數更新的步伐也較小
這樣有什麼好處呢?這代表 Loss function 在平緩的坡度時,學習率會越走越大,參數更新的步伐會越大,這樣就不會在一片平地中要迭代上萬次才能走到最佳解,另一方面如果 Loss function 在陡峭的坡度時,學習率會越走越小,參數更新的步伐會越小,這避免了每次參數更新步伐過大可能會在山谷中來回震盪的問題
範例
拿 上一篇文章的 Batch Gradient Descent 來當範例,當學習率 = 0.28 時會有來回震盪無法收斂的問題出現,而改用 AdaGrad 動態調整每次迭代的學習率後可以穩定的收斂

Batch Gradient Descent:學習率固定,來回震盪無法收斂

AdaGrad:自適應學習率,穩定收斂
小結
AdaGrad 是一個重要的自適應優化算法,它通過累積梯度平方和來動態調整每個參數的學習率,避免了每次參數更新步伐過大可能會在山谷中來回震盪的問題。但 AdaGrad 會有學習率過度衰減的問題,限制了其在深度學習中的廣泛應用,接著讓我們來看看如何利用 RMSProp 算法解決。
什麼是 RMSProp?
RMSProp(Root Mean Square Propagation) 是由 Geoffrey Hinton 在 2012 年提出的一種優化算法,它解決了 AdaGrad 學習率過度衰減的問題。RMSProp 使用 指數移動平均(Exponential Moving Average, EMA) 來替代 AdaGrad 中的梯度累積,這樣可以讓學習率在訓練過程中保持相對穩定。
數學表達式
RMSProp:
$$w_i^{t+1} = w_i^t - \frac{\eta}{\sqrt{\sigma_i^t + \epsilon}} \cdot g_i^t$$
這些參數代表的意思都跟 AdaGrad 相同:
- $w_i^{t+1}$ 是參數 $i$ 在第 $t+1$ 步的更新值
- $w_i^t$ 是參數 $i$ 在第 $t$ 步的當前值
- $\eta$ 是全局學習率
- $g_i^t$ 是參數 $i$ 在第 $t$ 步的梯度
- $\epsilon$ 是一個很小的常數(通常為 $10^{-8}$),用於避免分母除以零導致錯誤
- $\sigma_i^t$ 是參數 $i$ 在第 $t$ 步的梯度平方的指數移動平均
這裡的關鍵 $\sigma_i^t$ 計算的方式會使用 衰減率 $\alpha$ 控制歷史梯度的影響程度:
$$\sigma_i^t = \alpha \cdot \sigma_i^{t-1} + (1 - \alpha) \cdot (g_i^t)^2$$
其中:
- $\sigma_i^t$ 是參數 $i$ 在第 $t$ 步的梯度平方的指數移動平均
- $g_i^t$ 是參數 $i$ 在第 $t$ 步的梯度
- $\alpha$ 是衰減率(通常設為 0.9),控制歷史梯度的影響程度
實際上 指數移動平均 是怎麼計算的呢?一樣推薦 李宏毅老師講解 RMSProp 有清晰的講解
與 AdaGrad 的關鍵差異
AdaGrad 的問題:
$$G_i^t = G_i^{t-1} + (g_i^t)^2$$
AdaGrad 直接累積所有歷史梯度的平方,隨著訓練進行,$G_i^t$ 會越來越大,導致學習率 $\displaystyle \frac{\eta}{\sqrt{G_i^t + \epsilon}}$ 越來越小。
RMSProp 的解決方案:
$$\sigma_i^t = \alpha \cdot \sigma_i^{t-1} + (1 - \alpha) \cdot (g_i^t)^2$$
RMSProp 使用指數移動平均,很久之前的梯度權重會不斷乘以 $\alpha \approx 0.9$ 逐漸衰減,而最近的梯度佔有更大的權重。這樣 $\sigma_i^t$ 不會無限增長,學習率 $\displaystyle \frac{\eta}{\sqrt{\sigma_i^t + \epsilon}}$ 也能保持相對穩定。
學習率自適應
RMSProp 的學習率計算為:
$$\eta_{RMSProp} = \frac{\eta}{\sqrt{\sigma_i^t + \epsilon}}$$
由於 $\sigma_i^t$ 使用指數移動平均,它會自動「遺忘」很久以前的梯度信息,分母的值不會一直增大,因此學習率不會像 AdaGrad 那樣過度衰減。
範例
拿上面提到的 AdaGrad 與現在的 RMSProp 做範例,可以看到 AdaGrad 在迭代過程中學習率不斷降低使得每步走的步伐越來越小,要花更多時間走到最佳解的點,而 RMSProp 避免了學習率過度衰減的問題,可以快速地抵達最佳解

AdaGrad:學習率不斷降低,需要更多步伐走到終點

RMSProp:避免學習率過度衰減,快速走到終點
小結
RMSProp 通過引入指數移動平均解決了 AdaGrad 的學習率衰減問題,使得優化器在深度學習中表現更加穩定。它保持了自適應學習率的優勢,同時避免了後期訓練緩慢的問題。
什麼是 Adam?
Adam (Adaptive Moment Estimation) 是由 Diederik P. Kingma 和 Jimmy Ba 在 2014 年提出的一種優化算法,它結合了 Momentum 和 RMSProp 的優點。Adam 不僅具有自適應學習率的特性,還加入了動量機制,使得優化過程更加穩定和高效。
數學表達式
Adam:
$$w_i^{t+1} = w_i^t - \frac{\eta}{\sqrt{\hat{v}_i^t} + \epsilon} \cdot \hat{m}_i^t$$
其中 $\hat{m}_i^t$ 和 $\hat{v}_i^t$ 分別是偏差修正後的一階矩估計和二階矩估計:
$$\hat{m}_i^t = \frac{m_i^t}{1 - \beta_1^t}$$
$$\hat{v}_i^t = \frac{v_i^t}{1 - \beta_2^t}$$
而 $m_i^t$ 和 $v_i^t$ 分別是:
$$m_i^t = \beta_1 \cdot m_i^{t-1} + (1 - \beta_1) \cdot g_i^t$$
$$v_i^t = \beta_2 \cdot v_i^{t-1} + (1 - \beta_2) \cdot (g_i^t)^2$$
其中:
- $w_i^{t+1}$ 是參數 $i$ 在第 $t+1$ 步的更新值
- $w_i^t$ 是參數 $i$ 在第 $t$ 步的當前值
- $\eta$ 是全局學習率
- $g_i^t$ 是參數 $i$ 在第 $t$ 步的梯度
- $m_i^t$ 是參數 $i$ 在第 $t$ 步的一階矩估計(類似動量)
- $v_i^t$ 是參數 $i$ 在第 $t$ 步的二階矩估計(類似 RMSProp)
- $\beta_1$ 是一階矩的衰減率(通常設為 0.9)
- $\beta_2$ 是二階矩的衰減率(通常設為 0.999)
- $\epsilon$ 是一個很小的常數(通常為 $10^{-8}$),用於避免分母除以零
- $\hat{m}_i^t$ 和 $\hat{v}_i^t$ 是偏差修正後的估計值
Adam 的三大特點
1. 動量機制 (Momentum)
$$m_i^t = \beta_1 \cdot m_i^{t-1} + (1 - \beta_1) \cdot g_i^t$$
這部分類似於 Momentum 優化器,通過累積歷史梯度來加速收斂,特別是在平坦區域和狹長的山谷中。
2. 自適應學習率 (Adaptive Learning Rate)
$$v_i^t = \beta_2 \cdot v_i^{t-1} + (1 - \beta_2) \cdot (g_i^t)^2$$
這部分類似於 RMSProp,通過指數移動平均來調整每個參數的學習率。
3. 偏差修正 (Bias Correction)
$$\hat{m}_i^t = \frac{m_i^t}{1 - \beta_1^t}$$
$$\hat{v}_i^t = \frac{v_i^t}{1 - \beta_2^t}$$
分母的 $\beta_1^t$ 與 $\beta_2^t$ 指的是 $\beta$ 的 t 次方,由於 $m_i^t$ 和 $v_i^t$ 在訓練初期會偏向於 0,偏差修正可以讓估計值更準確。
- $\beta_1^t$ 與 $\beta_2^t$ 在前三次迭代的修正倍率
| t | β₁ᵗ | 1 - β₁ᵗ | β₁ 修正倍率 | β₂ᵗ | 1 - β₂ᵗ | β₂ 修正倍率 |
|---|---|---|---|---|---|---|
| 1 | 0.9 | 0.1 | 10.000000 | 0.999 | 0.001 | 1000.000000 |
| 2 | 0.81 | 0.19 | 5.263158 | 0.998001 | 0.001999 | 500.250125 |
| 3 | 0.729 | 0.271 | 3.688524 | 0.997003 | 0.002997 | 333.555851 |
範例
拿上面提到的 RMSProp 與現在的 Adam 做範例,可以看到 RMSProp 穩定走到終點,Adam 或許是引入動量的關係會稍微超過最佳解後再收斂回來 (迭代次數更多的話可以看到收斂回來)

RMSProp:穩定走到終點

Adam:稍微超過最佳解後再收斂回來
小結
Adam 優化器通過結合動量機制和自適應學習率,不僅解決了 AdaGrad 的學習率衰減問題,還加入了動量來加速收斂,同時通過偏差修正提高了訓練初期的穩定性,也因此成為了現今深度學習中默認的優化器。
總結
| 特性 | SGD | Momentum | AdaGrad | RMSProp | Adam |
|---|---|---|---|---|---|
| 動量 | ❌ | ✅ | ❌ | ❌ | ✅ |
| 自適應學習率 | ❌ | ❌ | ✅ | ✅ | ✅ |
| 偏差修正 | ❌ | ❌ | ❌ | ❌ | ✅ |
| 收斂速度 | 慢 | 中等 | 中等 | 快 | 最快 |
| 穩定性 | 低 | 中等 | 高 | 高 | 最高 |
參考資料
【機器學習 2021】類神經網路訓練不起來怎麼辦 (三):自動調整學習速率 (Learning Rate)
Optimization for Deep Learning (Momentum, RMSprop, AdaGrad, Adam)
機器/深度學習-基礎數學(三):梯度最佳解相關算法(gradient descent optimization algorithms)
[機器學習 ML NOTE]SGD, Momentum, AdaGrad, Adam Optimizer