此為 機器學習中的優化器 系列文章 - 第 2 篇:
- 機器學習中的優化器 (1) - Gradient descent 梯度下降與其變體
- 機器學習中的優化器 (2) - 從梯度下降問題到動量優化
- 機器學習中的優化器 (3) - AdaGrad、RMSProp 與 Adam
梯度下降面臨的問題
在上一篇 Gradient descent 梯度下降與其變體 文章中,我們介紹了梯度下降的基本原理和三種主要變形:Batch Gradient Descent、Stochastic Gradient Descent (SGD) 和 Mini-batch Gradient Descent。雖然這些方法在機器學習中發揮了重要作用,但在實際應用中仍然面臨一些挑戰:
1. 學習率選擇困難
問題描述:
- 學習率太小:收斂速度慢,需要大量迭代
- 學習率太大:可能導致震盪或發散
- 不同參數可能需要不同的學習率
數學表達:
$$w_{t+1} = w_t - \eta \nabla L(w_t)$$
其中 $\eta$ 是固定的學習率,但實際上:
- 在平坦區域需要較大學習率加速
- 在陡峭區域需要較小學習率避免震盪
範例:
以上一篇文章的 Batch gradient descent 為例,左圖學習率 $0.1$ 可以穩定收斂到 $w1=2, w2=2$ 的最佳權重,但如果學習率選擇過大 $0.28$,則會不斷震盪 loss 無法收斂到最小值:

學習率 η = 0.1:穩定收斂

學習率 η = 0.28:來回震盪無法收斂
2. 梯度消失與梯度爆炸
梯度消失 (Vanishing Gradient):
- 在深度網路中,梯度可能變得極小
- 導致早期層的參數更新緩慢
梯度爆炸 (Exploding Gradient):
- 梯度可能變得極大
- 導致參數更新過大,模型不穩定
範例:
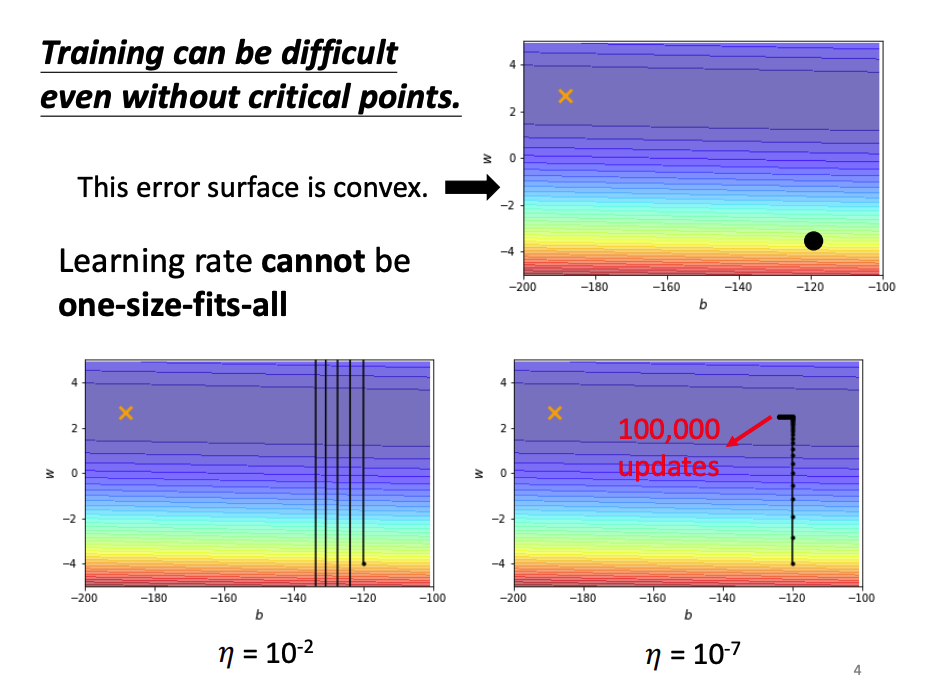
以下圖為例:橘色的 x 點是達到最佳解的位置,而黑色圓點是訓練起始點,左下圖設置學習率 $η = 10^{-2}$ 的結果是學習率設置過大導致 梯度爆炸,而右下圖設置學習率 $η = 10^{-7}$ 則又太小導致中間走了 100000 次迭代離最佳解的位置還很遠
Momentum 動量優化
為了解決上述問題,研究人員提出了多種優化算法。其中 Momentum 是最早且最有效的改進之一。
Momentum 的核心思想
Momentum 的靈感來自物理學中的動量概念。就像一個球在滾動時會保持一定的動量,Momentum 算法會累積之前的梯度方向,形成一種”慣性”。
Momentum 的視覺化理解
想像一個球在損失函數的表面上滾動:
- 標準梯度下降:球只受當前位置的坡度影響
- Momentum:球有慣性,會保持之前的方向,同時受當前坡度影響
這使得 Momentum 在以下情況特別有效:
- 狹長的山谷(減少震盪)
- 平坦區域(加速移動)
- 局部最小值(提供逃離的動能)
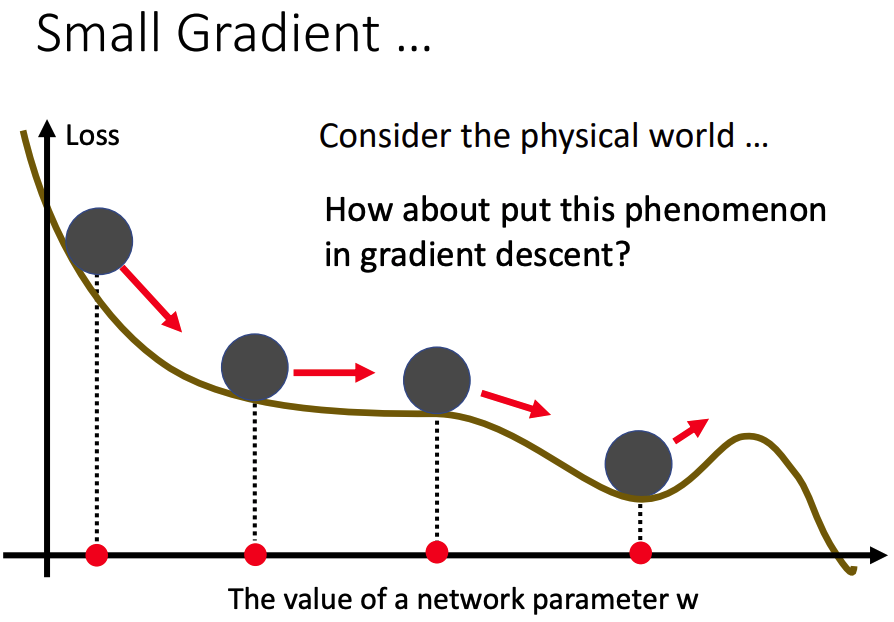
如下圖所示:在 Gradient descent 迭代的過程,不幸第四步走到了局部最小值(Local Minimum),但我們最終想要找到的最佳解是 全局最小值(Global Minimum) 也就是需要往圖中更右邊的地方尋找。但當走到圖中的山谷中,此時 Gradient descent 的值已經是 0 了無法再進行下一次迭代,而求出的解只是 局部最小值(Local Minimum)
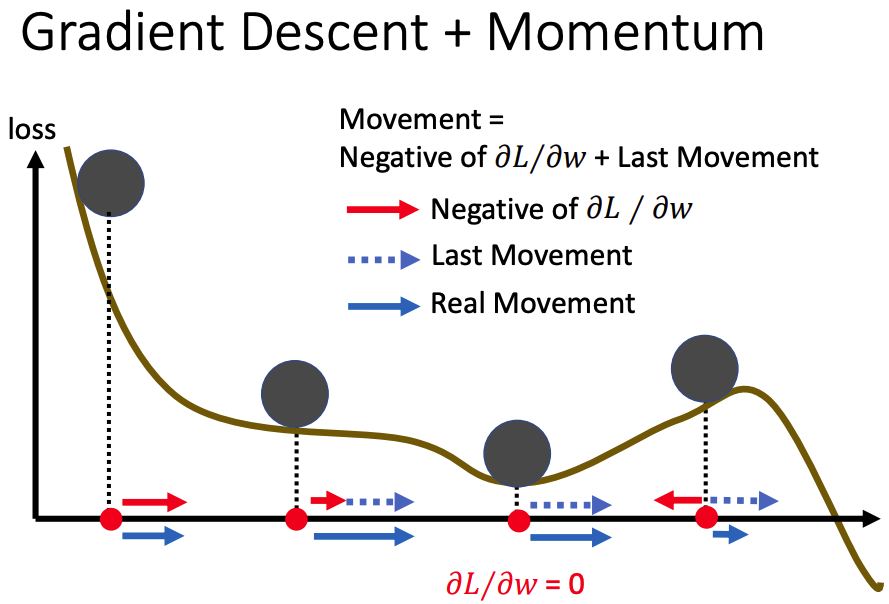
因此 Momentum 出現了,下圖的紅色箭頭代表使用 Gradient descent 計算出來下一次迭代該走的方向與大小,可以看到山谷中因為 Gradient descent 等於 0,所以並沒有紅色箭頭。虛線藍色箭頭代表 上一次迭代的移動 (Last Movement) 對於這一次迭代的影響,這個 Last Movement 就是 Momentum 的概念。藍色實線箭頭是將 Gradient descent 及 Momentum 都考慮進去後目前迭代實際前往的方向及大小
可以看到上圖原本在山谷中走不出去的狀況,現在有機會靠著 Momentum 在上一步保留的慣性往右走脫離山谷,往圖中右側繼續尋找 全局最小值(Global Minimum)
數學表達式
標準梯度下降:
$$w_{t+1} = w_t - \eta \nabla L(w_t)$$
其中:
- $w_t$ 是第 $t$ 步的權重
- $\eta$ 是學習率(步長)
- $\nabla L(w_t)$ 是損失函數在 $w_t$ 處的梯度
Momentum:
$$w_{t+1} = w_t + v_{t+1}$$
$$v_{t+1} = \beta v_t - \eta \nabla L(w_t)$$
其中:
- $v_{t+1}, v_t$ 代表 速度 (velocity) 項。
- $\beta$ 是 動量係數 (Momentum),控制每次迭代動量影響的大小,通常設定為 0.9
Momentum 計算:
以下兩部影片更完整地講解 Momentum 的計算
Momentum 的優勢
1. 加速收斂
在平坦區域:
- 梯度較小,但動量項會累積之前的方向
- 提供額外的推動力,加速收斂
在陡峭區域:
- 動量項會緩衝梯度的變化
- 減少震盪,提供更穩定的更新
2. 逃離局部最小值
- 動量項提供額外的 慣性
- 幫助算法跳出淺層的局部最小值
3. 減少震盪
- 在狹長的山谷中,標準梯度下降會來回震盪
- Momentum 會沿著山谷的方向加速移動
- 大幅減少震盪,提高收斂效率
Momentum 的參數選擇
動量係數 $\beta$:
- 通常設為 0.9
- $\beta$ 越大,動量效果越強
- $\beta$ 越小,越接近標準梯度下降
Momentum vs 標準梯度下降比較
| 特性 | 標準梯度下降 | Momentum |
|---|---|---|
| 收斂速度 | 較慢 | 較快 |
| 震盪 | 較多 | 較少 |
| 局部最小值 | 容易陷入 | 較易逃離 |
| 參數調整 | 學習率敏感 | 相對穩定 |
| 計算成本 | 低 | 稍高 |
結論
Momentum 通過引入動量項,有效解決了標準梯度下降的許多問題:
- 加速收斂:在平坦區域提供額外推動力
- 減少震盪:在狹長山谷中沿著正確方向加速
- 逃離局部最小值:提供額外的”慣性”動能
- 提高穩定性:緩衝梯度的變化
然而,Momentum 仍然有一些限制,例如:
- 對所有參數使用相同的學習率
- 無法自適應調整學習率
- 在某些情況下可能過度衝刺
這些問題將在下一篇文章的優化算法(如 AdaGrad、RMSprop 和 Adam)中得到進一步改善。
參考資料
【機器學習 2021】類神經網路訓練不起來怎麼辦 (二): 批次 (batch) 與動量 (momentum)
Optimization for Deep Learning (Momentum, RMSprop, AdaGrad, Adam)
機器/深度學習-基礎數學(三):梯度最佳解相關算法(gradient descent optimization algorithms)
[機器學習 ML NOTE]SGD, Momentum, AdaGrad, Adam Optimizer