此為 機器學習中的優化器 系列文章 - 第 1 篇:
- 機器學習中的優化器 (1) - Gradient descent 梯度下降與其變體
- 機器學習中的優化器 (2) - 從梯度下降問題到動量優化
- 機器學習中的優化器 (3) - AdaGrad、RMSProp 與 Adam
什麼是優化器 Optimizer?
在機器學習和深度學習中,優化器(Optimizer) 是訓練模型的核心組件。它的主要任務是找到一組最佳的模型參數,使得損失函數達到最小值,從而讓模型能夠做出最準確的預測,此篇文章所要介紹的 Gradient descent 就是其中一種優化器
為什麼需要 Gradient descent?
在機器學習與深度學習中,我們常要找到一組最佳的模型參數,使 損失函數 (Loss function) 達到最小值,此時找到最佳的權重參數 $w$ 使得預測值 $\hat{y}$ 與實際值 $y$ 之間的誤差最小,這代表模型在預測時的誤差最小,預測效果最佳。而 梯度下降 (Gradient descent) 則是在尋找 損失函數 (Loss function) 最小值過程中的一個關鍵技術。
Gradient descent 扮演的角色
機器學習模型通常有很多 參數(權重),這些參數需要不斷調整,以減少模型預測結果與真實標籤之間的誤差。
損失函數是一個關於這些參數的函數,我們希望找到能使此函數值最小的參數組合,這對應到最佳模型。
直接求解損失函數的最小值通常非常困難,尤其當模型複雜、參數眾多時,求解析解不現實。
梯度下降是一種迭代優化算法,透過計算 損失函數 對參數的 梯度(偏微分),告訴我們在參數空間中 “下降最快的方向”。
每一步,模型參數沿著梯度的反方向(即使損失下降的方向)調整一點點,逐步逼近損失函數的最低點,進而得到最佳參數。
透過反覆迭代這個過程,可以自動化尋找最佳模型參數,讓模型的預測誤差最小。
核心思想
梯度下降的基本思想是:
- 在當前點計算函數的梯度(偏導數)
- 沿著梯度的反方向移動一小步
- 重複這個過程,直到收斂到局部最小值
數學表達式:
$$w_{t+1} = w_t - \eta \nabla L(w_t)$$
其中:
- $w_t$ 是第 $t$ 步的權重
- $\eta$ 是學習率(步長)
- $\nabla L(w_t)$ 是損失函數在 $w_t$ 處的梯度
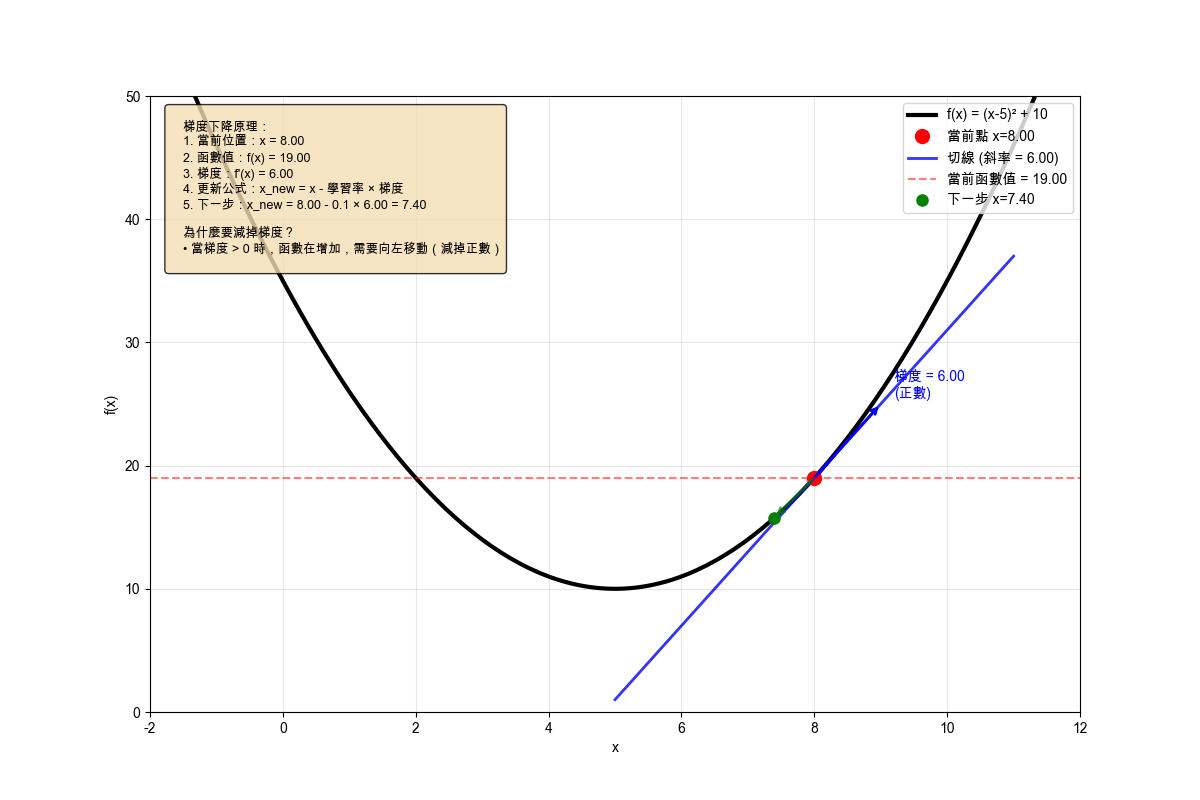
為什麼沿著梯度反方向?
梯度 $\nabla L(w)$ 指向函數增長的方向,因此沿著梯度的反方向 $- \nabla L(w)$ 移動就是朝著函數值減小的方向前進,以下圖為例:在 $ x = 8 $ 的點,求得梯度值為 6,而我們希望的是函數值 $f(x)$ 逐步變小,所以需要將當下的 $x$ 減去 梯度值求得下一步的 $x$
Gradient descent 的三種變形
在機器學習中,根據每次更新參數時使用的資料量,可以將 Gradient Descent 分為三種主要變形:
1. Batch Gradient Descent(批次梯度下降 BGD)
特點:
- 每次迭代使用 所有訓練資料 來計算梯度
- 梯度計算最穩定,但計算成本最高
- 適合資料集較小的情況
數學表達式:
$$w_{t+1} = w_t - \eta \cdot \frac{1}{N} \sum_{i=1}^{N} \nabla L(w_t, x^{(i)}, y^{(i)})$$
其中 $N$ 是訓練資料總數。
優點:
- 梯度估計最準確
- 收斂路徑平滑
- 理論保證收斂到局部最小值
缺點:
- 計算成本高
- 記憶體需求大
- 不適合大資料集
2. Stochastic Gradient Descent(隨機梯度下降 SGD)
特點:
- 每次迭代只使用 一筆訓練資料 來計算梯度
- 計算速度快,但梯度估計較不穩定
- 適合大資料集
- 收斂路徑較不規則
數學表達式:
$$w_{t+1} = w_t - \eta \cdot \nabla L(w_t, x^{(i)}, y^{(i)})$$
其中 $i$ 是隨機選擇的資料索引。
優點:
- 計算速度快
- 記憶體需求小
- 可以逃離局部最小值
- 適合大資料集
缺點:
- 梯度估計不穩定
- 收斂路徑不規則
- 需要調整學習率
3. Mini-batch Gradient Descent(小批次梯度下降)
特點:
- 每次迭代使用 一小批訓練資料 來計算梯度
- 結合了 BGD 和 SGD 的優點
- 最常用的梯度下降方法
- 收斂路徑介於兩者之間
數學表達式:
$$w_{t+1} = w_t - \eta \cdot \frac{1}{B} \sum_{i \in \mathcal{B}} \nabla L(w_t, x^{(i)}, y^{(i)})$$
其中 $B$ 是小批次大小,$\mathcal{B}$ 是當前批次中的資料索引。
優點:
- 計算效率高
- 梯度估計相對穩定
- 記憶體需求適中
- 適合各種資料集大小
缺點:
- 需要調整批次大小
- 收斂路徑不如 BGD 平滑
三種方法的比較
| 方法 | 批次大小 | 梯度穩定性 | 計算速度 | 記憶體需求 | 適用場景 |
|---|---|---|---|---|---|
| BGD | 全部資料 | 最穩定 | 最慢 | 最高 | 小資料集 |
| SGD | 1 筆資料 | 最不穩定 | 最快 | 最低 | 大資料集 |
| Mini-batch GD | 小批次 | 中等 | 中等 | 中等 | 通用 |
選擇建議
- 小資料集(< 1000 筆):使用 BGD
- 大資料集(> 10000 筆):使用 Mini-batch GD
- 超大資料集(> 100000 筆):使用 SGD
- 一般情況:推薦使用 Mini-batch GD,批次大小通常設為 32、64 或 128
以下藉由計算 Batch Gradient descent 跟 Stochastic Gradient Descent 來體會使用不同 Gradient descent 處理資料的差別
Batch Gradient Descent 範例
模型設定
假設我們現在打算使用 Batch Gradient Descent 對一個簡單的線性模型求解:
$$\hat{y} = w_1 x_1 + w_2 x_2$$
其中:
• 輸入:$ x = [x_1, x_2] $
• 權重:$ w = [w_1, w_2] $
• 預測:$ \hat{y} = w_1 x_1 + w_2 x_2 $
• 實際值:$ y $
目標是讓 $\hat{y}$ 趨近於實際值 $y$。我們使用三筆訓練資料:
• 資料 1:$x_1 = 1$, $x_2 = 1$, $y = 4$
• 資料 2:$x_1 = 2$, $x_2 = 1$, $y = 6$
• 資料 3:$x_1 = 1$, $x_2 = 2$, $y = 6$
損失函數 Loss
對於多筆資料,損失函數是所有資料的平方誤差總和的平均值:
$$L(w_1, w_2) = \frac{1}{3} \sum_{i=1}^{3} (y^{(i)} - \hat{y}^{(i)})^2$$
其中 $\hat{y}^{(i)} = w_1 x_1^{(i)} + w_2 x_2^{(i)}$
展開後:
$$L(w_1, w_2) = \frac{1}{3} \left[(4 - (w_1 + w_2))^2 + (6 - (2w_1 + w_2))^2 + (6 - (w_1 + 2w_2))^2\right]$$
梯度計算
對 $w_1$ 求偏導:
$$\frac{\partial L}{\partial w_1} = \frac{1}{3} \left[-2(4 - w_1 - w_2) - 4(6 - 2w_1 - w_2) - 2(6 - w_1 - 2w_2)\right]$$
對 $w_2$ 求偏導:
$$\frac{\partial L}{\partial w_2} = \frac{1}{3} \left[-2(4 - w_1 - w_2) - 2(6 - 2w_1 - w_2) - 4(6 - w_1 - 2w_2)\right]$$
選定初始值與學習率
• 初始值:$w_1 = 0$, $w_2 = 0$
• 學習率:$\eta = 0.1$
第一次迭代
預測值:
- 資料 1:$\hat{y}^{(1)} = 0 + 0 = 0$
- 資料 2:$\hat{y}^{(2)} = 0 + 0 = 0$
- 資料 3:$\hat{y}^{(3)} = 0 + 0 = 0$
Loss:
$$L = \frac{1}{3} \left[(4-0)^2 + (6-0)^2 + (6-0)^2\right] = \frac{1}{3}(16 + 36 + 36) = \frac{88}{3} \approx 29.33$$
梯度:
$$\frac{\partial L}{\partial w_1} = \frac{1}{3} \left[-2(4) - 4(6) - 2(6)\right] = \frac{1}{3}(-8 - 24 - 12) = \frac{-44}{3} \approx -14.67$$
$$\frac{\partial L}{\partial w_2} = \frac{1}{3} \left[-2(4) - 2(6) - 4(6)\right] = \frac{1}{3}(-8 - 12 - 24) = \frac{-44}{3} \approx -14.67$$
更新參數:
$$w_1^{(1)} = 0 - 0.1 \cdot \left(-\frac{44}{3}\right) = 0 + 0.1 \cdot \frac{44}{3} \approx 1.47$$
$$w_2^{(1)} = 0 - 0.1 \cdot \left(-\frac{44}{3}\right) = 0 + 0.1 \cdot \frac{44}{3} \approx 1.47$$
第二次迭代
此時 $w_1 = 1.47$, $w_2 = 1.47$
預測值:
- 資料 1:$\hat{y}^{(1)} = 1.47 + 1.47 = 2.94$
- 資料 2:$\hat{y}^{(2)} = 2 \cdot 1.47 + 1.47 = 4.41$
- 資料 3:$\hat{y}^{(3)} = 1.47 + 2 \cdot 1.47 = 4.41$
Loss:
$$L = \frac{1}{3} \left[(4-2.94)^2 + (6-4.41)^2 + (6-4.41)^2\right] = \frac{1}{3}(1.12 + 2.53 + 2.53) = \frac{6.18}{3} \approx 2.06$$
梯度:
$$\frac{\partial L}{\partial w_1} = \frac{1}{3} \left[-2(4-2.94) - 4(6-4.41) - 2(6-4.41)\right] = \frac{1}{3}(-2.12 - 6.36 - 3.18) = \frac{-11.66}{3} \approx -3.89$$
$$\frac{\partial L}{\partial w_2} = \frac{1}{3} \left[-2(4-2.94) - 2(6-4.41) - 4(6-4.41)\right] = \frac{1}{3}(-2.12 - 3.18 - 6.36) = \frac{-11.66}{3} \approx -3.89$$
更新參數:
$$w_1^{(2)} = 1.47 - 0.1 \cdot \left(-\frac{11.66}{3}\right) = 1.47 + 0.1 \cdot \frac{11.66}{3} \approx 1.86$$
$$w_2^{(2)} = 1.47 - 0.1 \cdot \left(-\frac{11.66}{3}\right) = 1.47 + 0.1 \cdot \frac{11.66}{3} \approx 1.86$$
第三次迭代
此時 $w_1 = 1.86$, $w_2 = 1.86$
預測值:
- 資料 1:$\hat{y}^{(1)} = 1.86 + 1.86 = 3.72$
- 資料 2:$\hat{y}^{(2)} = 2 \cdot 1.86 + 1.86 = 5.58$
- 資料 3:$\hat{y}^{(3)} = 1.86 + 2 \cdot 1.86 = 5.58$
Loss:
$$L = \frac{1}{3} \left[(4-3.72)^2 + (6-5.58)^2 + (6-5.58)^2\right] = \frac{1}{3}(0.0784 + 0.1764 + 0.1764) = \frac{0.4312}{3} \approx 0.144$$
梯度:
$$\frac{\partial L}{\partial w_1} = \frac{1}{3} \left[-2(4-3.72) - 4(6-5.58) - 2(6-5.58)\right] = \frac{1}{3}(-0.56 - 1.68 - 0.84) = \frac{-3.08}{3} \approx -1.027$$
$$\frac{\partial L}{\partial w_2} = \frac{1}{3} \left[-2(4-3.72) - 2(6-5.58) - 4(6-5.58)\right] = \frac{1}{3}(-0.56 - 0.84 - 1.68) = \frac{-3.08}{3} \approx -1.027$$
更新參數:
$$w_1^{(3)} = 1.86 - 0.1 \cdot \left(-\frac{3.08}{3}\right) = 1.86 + 0.1 \cdot \frac{3.08}{3} \approx 1.963$$
$$w_2^{(3)} = 1.86 - 0.1 \cdot \left(-\frac{3.08}{3}\right) = 1.86 + 0.1 \cdot \frac{3.08}{3} \approx 1.963$$
觀察收斂趨勢
可以看到:
- 第一次迭代:Loss ≈ 29.33
- 第二次迭代:Loss ≈ 2.06
- 第三次迭代:Loss ≈ 0.144
預測值逐漸接近目標值,Loss 也在持續下降,收斂路徑平滑穩定,權重迅速收斂到最佳解 $w_1 = 2$, $w_2 = 2$。
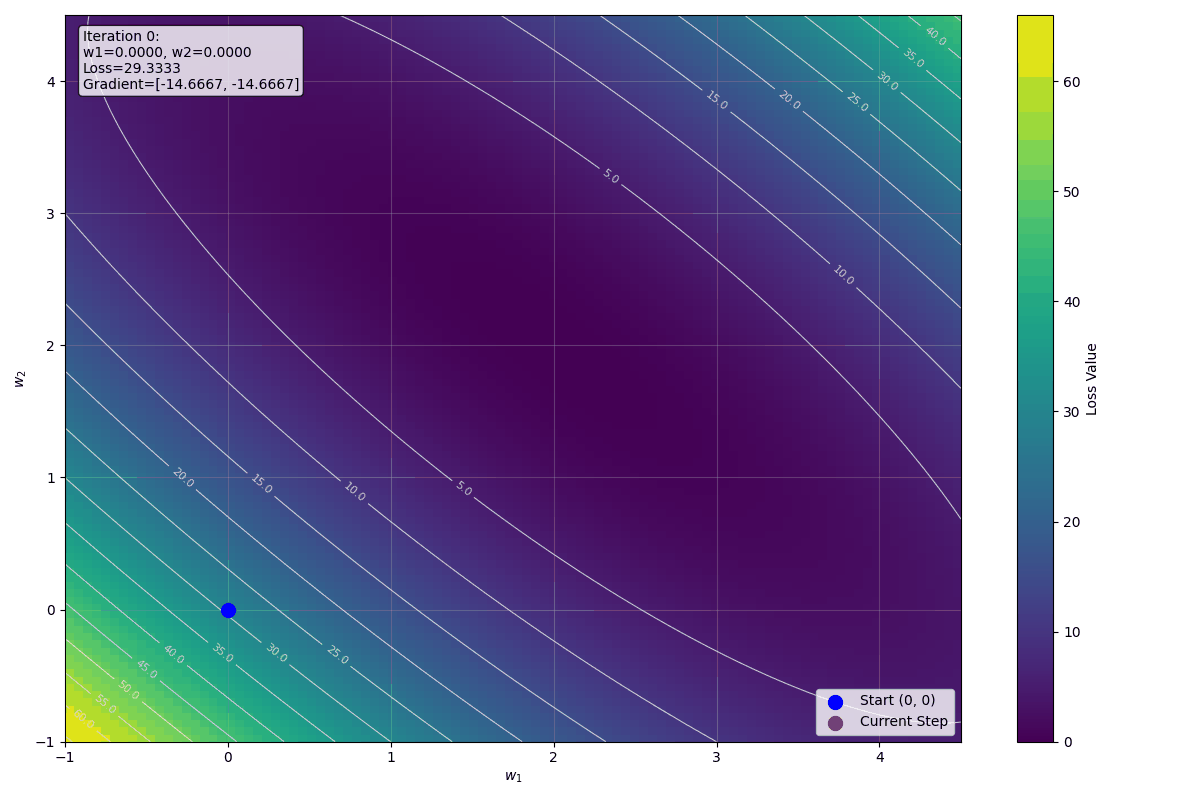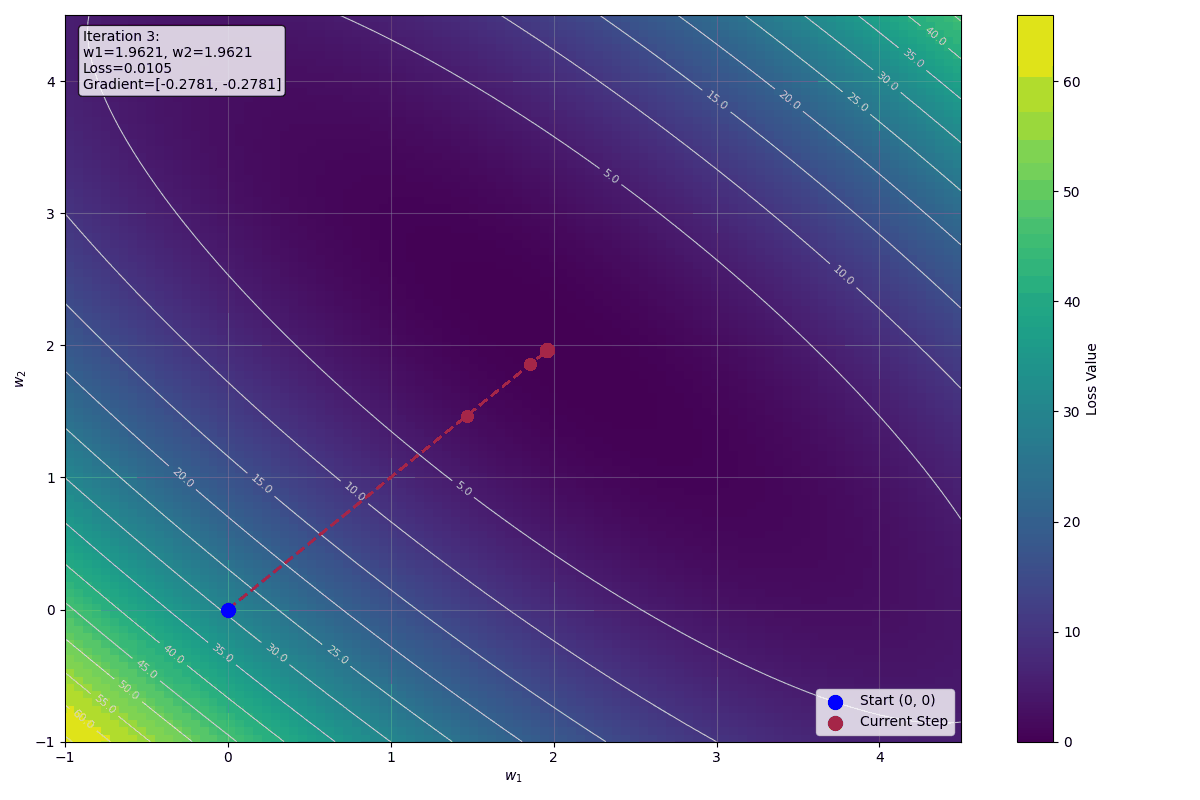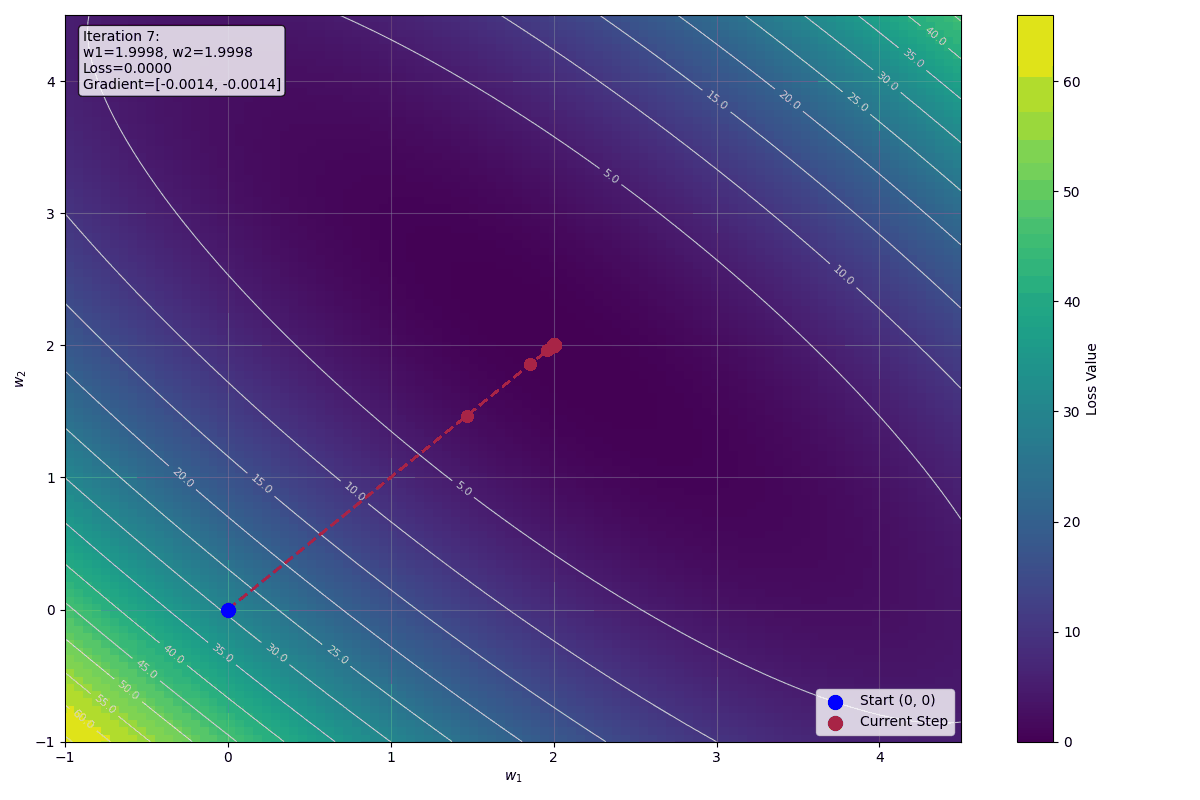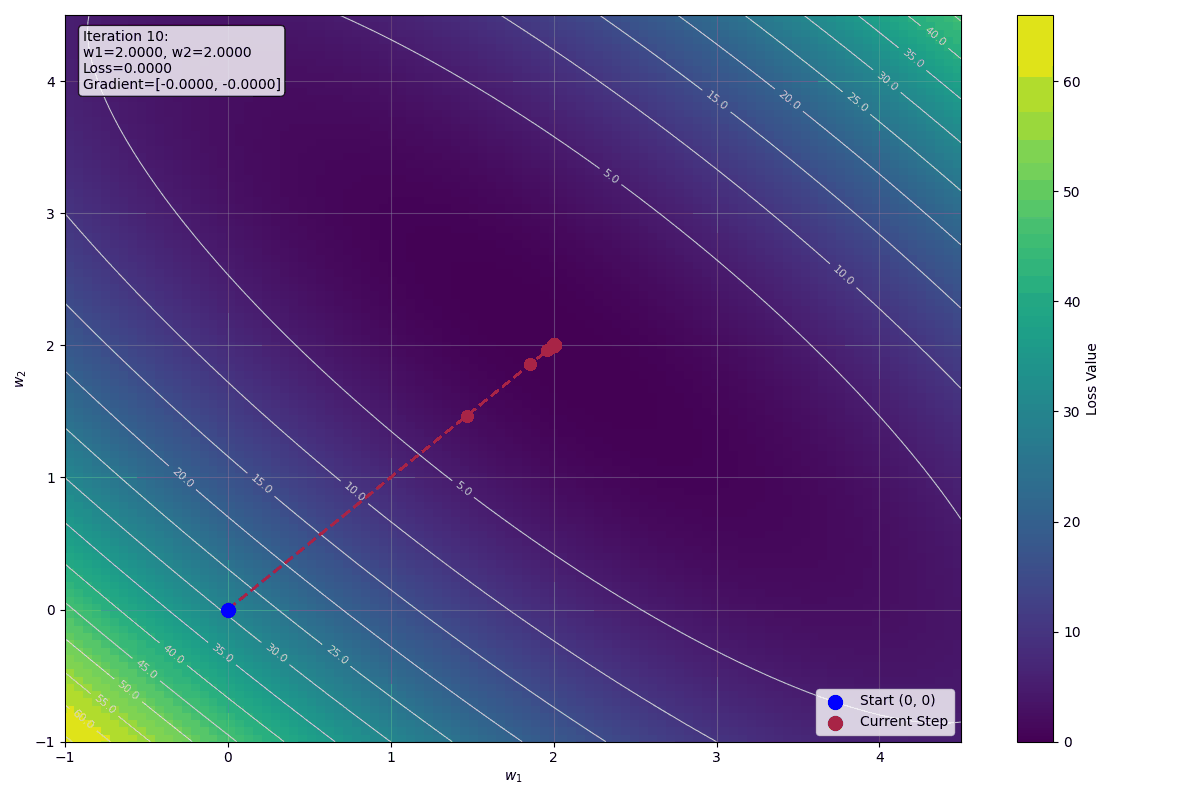
下圖顯示前十步迭代的視覺化影像:
Stochastic Gradient Descent (SGD) 範例
模型設定
使用相同的線性模型,但每次迭代使用不同的資料來示範 SGD:
$$\hat{y} = w_1 x_1 + w_2 x_2$$
其中:
• 輸入:$ x = [x_1, x_2] $
• 權重:$ w = [w_1, w_2] $
• 預測:$ \hat{y} = w_1 x_1 + w_2 x_2 $
• 實際值:$ y $
我們使用三筆訓練資料,每次迭代使用一筆不同的資料,這裡我們假設前三次迭代使用到的資料依序剛好都是 1, 2, 3:
• 資料 1:$x_1 = 1$, $x_2 = 1$, $y = 4$
• 資料 2:$x_1 = 2$, $x_2 = 1$, $y = 6$
• 資料 3:$x_1 = 1$, $x_2 = 2$, $y = 6$
損失函數 Loss
每次迭代使用單筆資料的平方誤差 (L2 Loss):
$$L(w_1, w_2) = (y^{(i)} - \hat{y}^{(i)})^2 = (y^{(i)} - (w_1 x_1^{(i)} + w_2 x_2^{(i)}))^2$$
其中 $i$ 是當前迭代使用的資料索引。
選定初始值與學習率
• 初始值:$w_1 = 0$, $w_2 = 0$
• 學習率:$\eta = 0.1$
第一次迭代:使用資料 1
資料:$x_1 = 1$, $x_2 = 1$, $y = 4$
預測:
$$\hat{y}^{(1)} = w_1^{(1)} + w_2^{(1)} = 0 + 0 = 0$$
Loss:
$$L^{(1)} = (4 - 0)^2 = 16$$
梯度計算:
對 $w_1$ 求偏導:
$$\frac{\partial L}{\partial w_1} = \frac{\partial}{\partial w_1} \left(4 - (w_1 + w_2)\right)^2 = -2(4 - w_1 - w_2) = -2(4 - 0 - 0) = -8$$
對 $w_2$ 求偏導:
$$\frac{\partial L}{\partial w_2} = \frac{\partial}{\partial w_2} \left(4 - (w_1 + w_2)\right)^2 = -2(4 - w_1 - w_2) = -2(4 - 0 - 0) = -8$$
更新參數:
$$w_1^{(2)} = w_1^{(1)} - \eta \cdot \frac{\partial L}{\partial w_1} = 0 - 0.1 \cdot (-8) = 0.8$$
$$w_2^{(2)} = w_2^{(1)} - \eta \cdot \frac{\partial L}{\partial w_2} = 0 - 0.1 \cdot (-8) = 0.8$$
第二次迭代:使用資料 2
資料:$x_1 = 2$, $x_2 = 1$, $y = 6$
此時 $w_1 = 0.8$, $w_2 = 0.8$
預測:
$$\hat{y}^{(2)} = 2 \cdot w_1^{(2)} + w_2^{(2)} = 2 \cdot 0.8 + 0.8 = 2.4$$
Loss:
$$L^{(2)} = (6 - 2.4)^2 = (3.6)^2 = 12.96$$
梯度計算:
對 $w_1$ 求偏導:
$$\frac{\partial L}{\partial w_1} = \frac{\partial}{\partial w_1} \left(6 - (2w_1 + w_2)\right)^2 = -4(6 - 2w_1 - w_2) = -4(6 - 2 \cdot 0.8 - 0.8) = -4(3.6) = -14.4$$
對 $w_2$ 求偏導:
$$\frac{\partial L}{\partial w_2} = \frac{\partial}{\partial w_2} \left(6 - (2w_1 + w_2)\right)^2 = -2(6 - 2w_1 - w_2) = -2(6 - 2 \cdot 0.8 - 0.8) = -2(3.6) = -7.2$$
更新參數:
$$w_1^{(3)} = w_1^{(2)} - \eta \cdot \frac{\partial L}{\partial w_1} = 0.8 - 0.1 \cdot (-14.4) = 0.8 + 1.44 = 2.24$$
$$w_2^{(3)} = w_2^{(2)} - \eta \cdot \frac{\partial L}{\partial w_2} = 0.8 - 0.1 \cdot (-7.2) = 0.8 + 0.72 = 1.52$$
第三次迭代:使用資料 3
資料:$x_1 = 1$, $x_2 = 2$, $y = 6$
此時 $w_1 = 2.24$, $w_2 = 1.52$
預測:
$$\hat{y}^{(3)} = w_1^{(3)} + 2 \cdot w_2^{(3)} = 2.24 + 2 \cdot 1.52 = 2.24 + 3.04 = 5.28$$
Loss:
$$L^{(3)} = (6 - 5.28)^2 = (0.72)^2 = 0.5184$$
梯度計算:
對 $w_1$ 求偏導:
$$\frac{\partial L}{\partial w_1} = \frac{\partial}{\partial w_1} \left(6 - (w_1 + 2w_2)\right)^2 = -2(6 - w_1 - 2w_2) = -2(6 - 2.24 - 2 \cdot 1.52) = -2(0.72) = -1.44$$
對 $w_2$ 求偏導:
$$\frac{\partial L}{\partial w_2} = \frac{\partial}{\partial w_2} \left(6 - (w_1 + 2w_2)\right)^2 = -4(6 - w_1 - 2w_2) = -4(6 - 2.24 - 2 \cdot 1.52) = -4(0.72) = -2.88$$
更新參數:
$$w_1^{(4)} = w_1^{(3)} - \eta \cdot \frac{\partial L}{\partial w_1} = 2.24 - 0.1 \cdot (-1.44) = 2.24 + 0.144 = 2.384$$
$$w_2^{(4)} = w_2^{(3)} - \eta \cdot \frac{\partial L}{\partial w_2} = 1.52 - 0.1 \cdot (-2.88) = 1.52 + 0.288 = 1.808$$
觀察收斂趨勢
可以看到 SGD 的迭代過程:
- 第一次迭代(資料 1):$w_1 = 0.8$, $w_2 = 0.8$, Loss = 16
- 第二次迭代(資料 2):$w_1 = 2.24$, $w_2 = 1.52$, Loss = 12.96
- 第三次迭代(資料 3):$w_1 = 2.384$, $w_2 = 1.808$, Loss = 0.5184
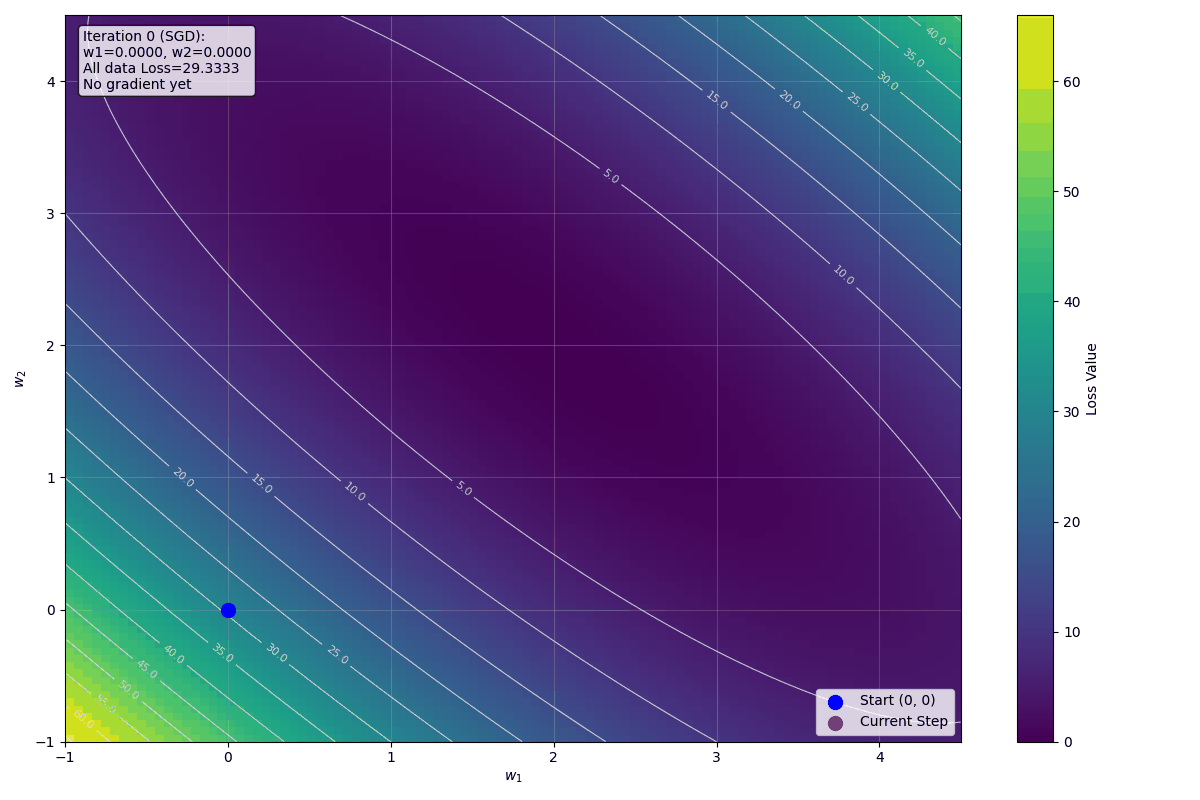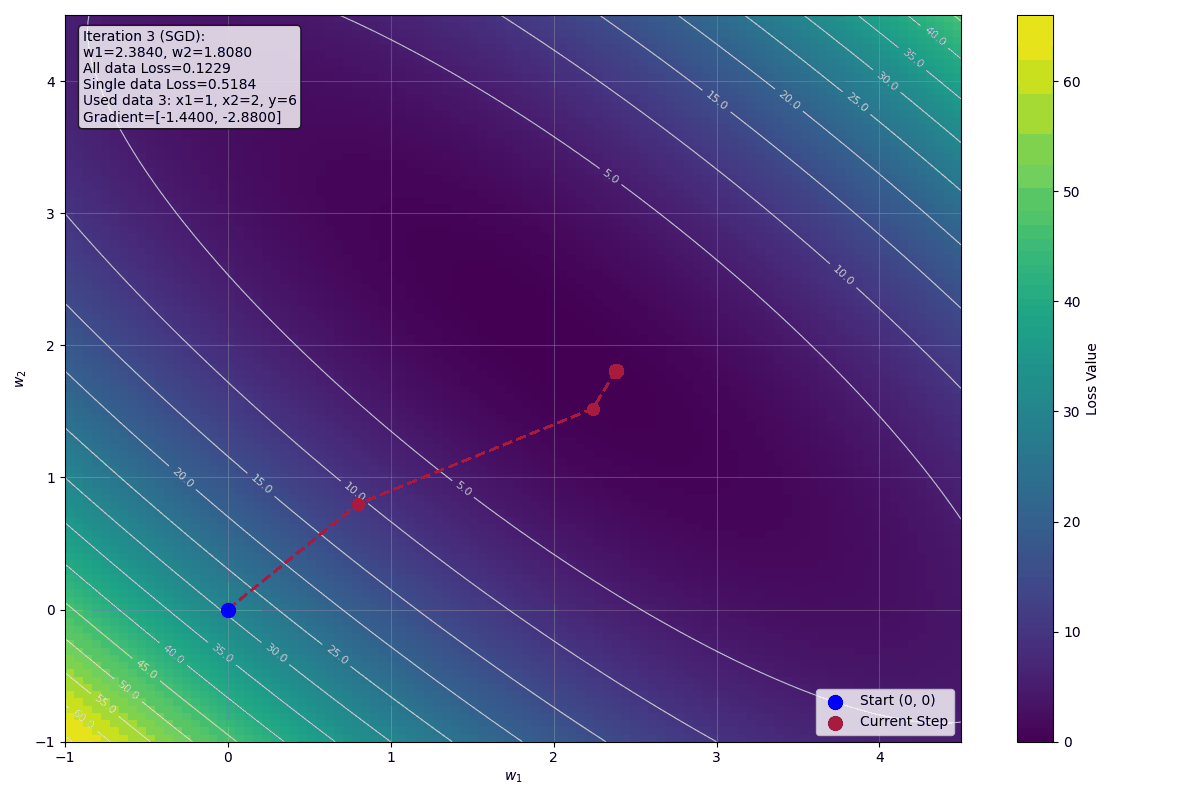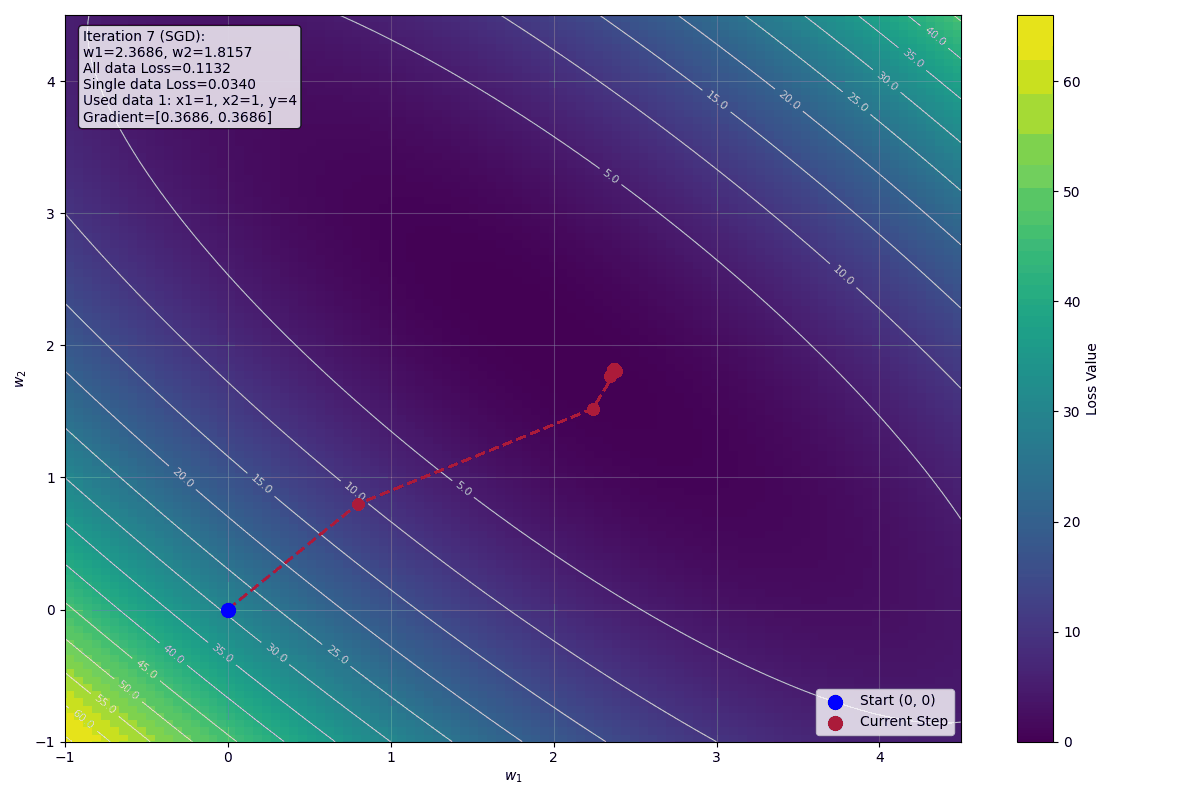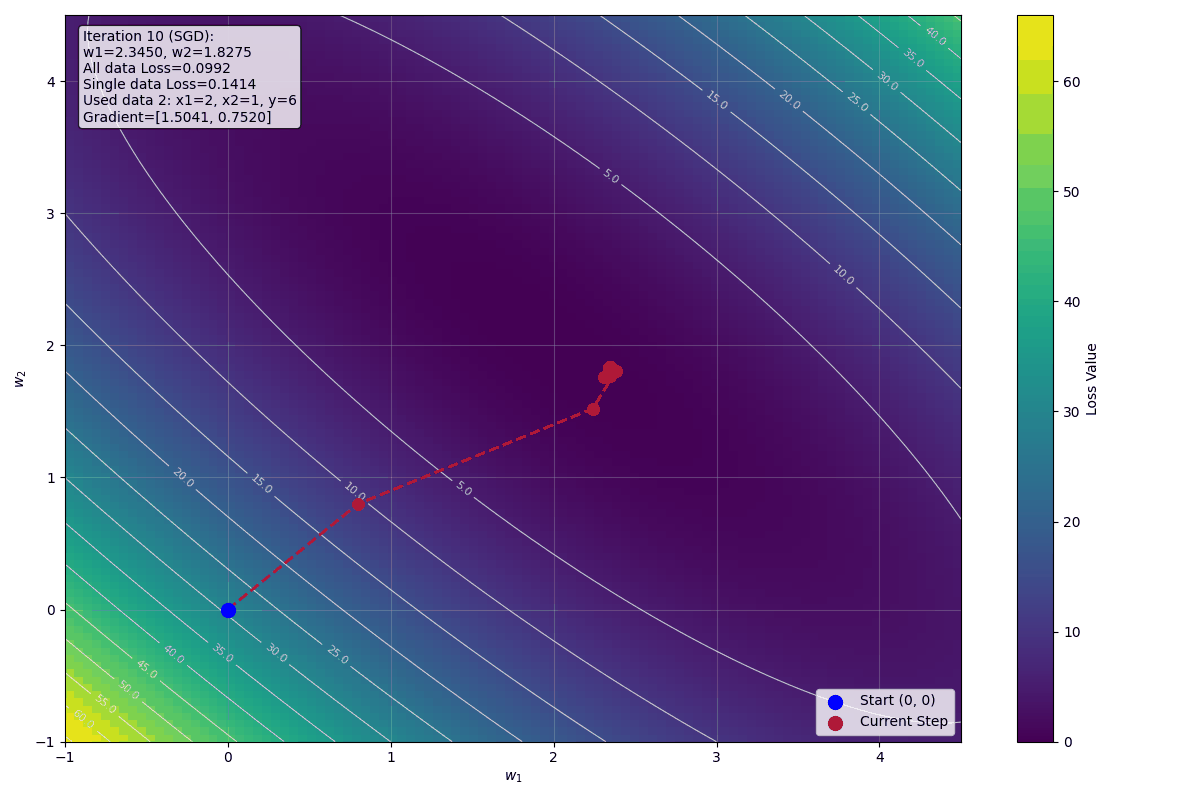
每次迭代使用不同的資料,權重緩慢接近最佳解 $w_1 = 2$, $w_2 = 2$。
下圖顯示前十步迭代的視覺化影像:
Batch Gradient Descent vs Stochastic Gradient Descent (SGD) 比較
Batch Gradient Descent
Batch Gradient Descent 會使用 所有訓練資料 來計算梯度,然後更新參數。這意味著:
- 每次更新參數時,都會考慮所有訓練資料的貢獻
- 梯度計算更穩定,但計算成本較高
- 適合資料集較小的情況
Stochastic Gradient Descent (SGD)
SGD 每次只使用 一筆訓練資料 來計算梯度並更新參數:
- 每次更新只考慮一筆資料
- 計算速度快,但梯度估計較不穩定
- 適合大資料集
主要差異
可以看到 Batch Gradient Descent 與 SGD 的主要差異:
- 梯度計算:BGD 考慮所有資料的貢獻,但除以資料總數得到平均梯度
- 收斂行為:BGD 的收斂路徑更平滑,梯度值較小且穩定
- 計算成本:每次迭代需要計算所有資料的梯度
- Loss 規模:平均損失函數的數值較小,更容易解釋
參考資料
Gradient descent 梯度下降
Learning Model : Gradient Descent 介紹與數學原理 [轉錄]