前言
L1 Loss 和 L2 Loss 是兩種常用的損失函數(Loss Function),主要用於衡量模型預測值與真實值之間的誤差,尤其廣泛用於回歸問題。
平均絕對誤差 (L1 Loss, MAE)
L1 Loss(Mean Absolute Error, MAE) 計算預測值與真實值誤差的 絕對值 的平均。
公式:
$$
\text{MAE} = \frac{1}{n} \sum_{i=1}^n |y_i - \hat{y}_i|
$$
- $y_i$:真實值
- $\hat{y}_i$:預測值
- $n$:樣本數
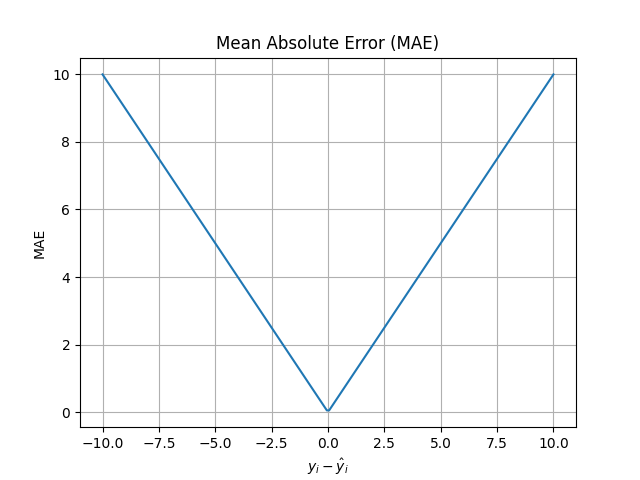
上圖展示了 MAE(平均絕對誤差)損失函數的曲線。
- x 軸:表示預測值與真實值之間的誤差($y_i - \hat{y}_i$)。
- y 軸:表示對應的損失值(MAE Loss)。
可以看到,MAE 的損失曲線是一條 V 形線,隨著誤差的增大,損失值以線性速度上升。這也說明了 MAE 對於離群值不會像 MSE 那樣放大誤差,較不會被離群值影響。
特性:
- 對於離群值(outlier)不敏感,因為誤差不會被平方放大。
- 反映預測誤差的實際大小,單位與原始資料相同。
- 對於所有誤差一視同仁,無論誤差大小。
均方誤差(L2 Loss, MSE)
L2 Loss(Mean Squared Error, MSE)則是將預測值與真實值之間的 誤差平方 後再取平均。
公式:
$$
\text{MSE} = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2
$$
- $y_i$:真實值
- $\hat{y}_i$:預測值
- $n$:樣本數
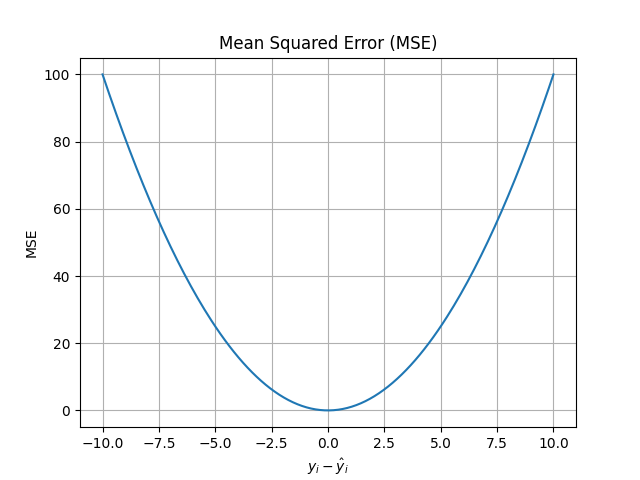
上圖展示了 MSE(均方誤差)損失函數的曲線。
- x 軸:表示預測值與真實值之間的誤差($y - \hat{y}$)。
- y 軸:表示對應的損失值(MSE Loss)。
可以看到,隨著誤差的增大,損失值會以平方的速度快速上升,這也是 L2 Loss 對離群值特別敏感的原因。
特性:
- 對於離群值非常敏感,因為誤差會被平方放大。
- 使得模型在訓練時更傾向於減少大誤差。
- 單位為原始資料單位的平方。
L1 Loss 與 L2 Loss 的比較
| 項目 | L1 Loss (MAE) | L2 Loss (MSE) |
|---|---|---|
| 定義 | 平均絕對誤差 | 平均平方誤差 |
| 對離群值敏感度 | 低 | 高 |
| 優點 | 對離群值不敏感 | 強調大誤差,數學性質好 |
| 缺點 | 誤差為 0 時不可微 | 對離群值過度敏感 |
| 適用情境 | 資料含離群值多時 | 資料較乾淨、需懲罰大誤差 |
選擇建議與應用
- L1 Loss 適合資料中存在離群值(outlier)時,或希望模型對異常值不那麼敏感。
- L2 Loss 適合資料較乾淨、希望模型對大誤差進行嚴格懲罰時。
小結
L1 Loss 與 L2 Loss 各有優缺點,選擇時需根據資料特性與應用需求做取捨。理解兩者的數學性質與實務影響,有助於設計更合適的模型與損失函數。